Turing Machines
Summarized notes from Introduction to Theory of Computation, Chapter 3
Differ from finite automata in following ways:
-
can read and write on the tape
-
read-write head can move left and right
-
the tape is infinite (unrestricted and unlimited memory access)
-
accepting and rejecting states take effect immediately
-
configuration: { current state, tape symbol, head location }
- can be written as \(uqv\) where current state is \(q\), current tape content is \(uv\) and current head location is the first symbol of \(v\), e.g. \(1011q_70111\)
- evaluation of input has 3 possible outcomes: accept, reject, or loop
- decider machines always halt and either accept or reject
- the language recognized by \(M\) is \(L(M)\)
- \(M\) accepts input \(w\) is a sequence of configurations \(C_1, C_2, \dots, C_k\) exists where
- \(C_1\) is the start configuration of \(M\) on input \(w\)
- each \(C_i\) yields \(C_{i+1}\)
- \(C_k\) is an accepting configuration
Formal Definition
It is not typical to define TM in this level of detail; it is sufficient to describe the operations of the machine or simply the algorithm and trust that the machine can simulate it.
7-tuple \(M = (Q, \Sigma, \Gamma, \delta, q_0, q_{\text{accept}}, q_{\text{reject}})\) where
| \(Q\) | finite set of states |
| \(\Sigma\) | finite input alphabet (without blank symbol) |
| \(\Gamma\) | finite tape alphabet (includes blank symbol and \(\Sigma \subseteq \Gamma\) |
| \(\delta: Q \times \Gamma \rightarrow Q \times \Gamma \times \{L, R\}\) | transition function |
| \(q_0 \in Q\) | start state |
| \(q_{\text{accept}} \in Q\) | accept state |
| \(q_{\text{reject}} \in Q\) | reject state \(q_{\text{accept}} \neq q_{\text{reject}}\) |
Recognizers and deciders
Turing-recognizable
A language is Turing-recognizable if some Turing machine recognizes it.
decidable
A language is decidable if some Turing machine decides it.
Notes:
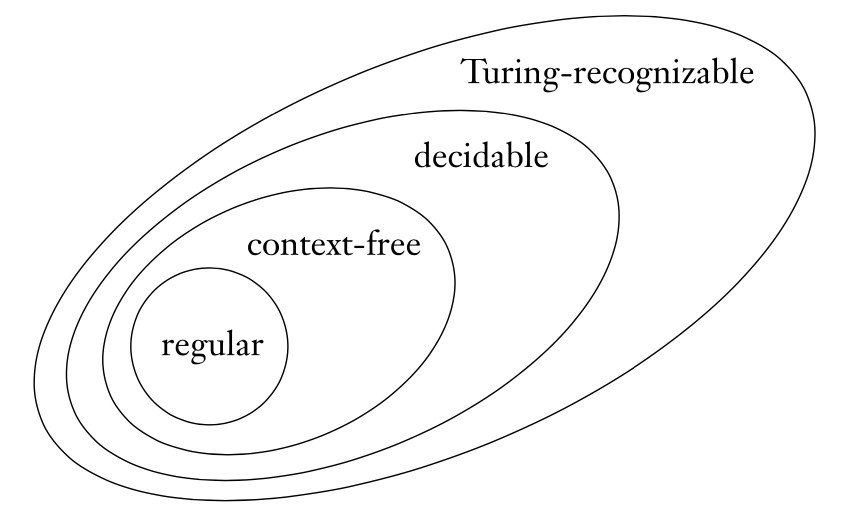
- every decidable language is Turing-recognizable
- recognizers are more powerful than deciders
- if both a language and its complement are Turing-recognizable, the language is decidable
- language is co-Turing-recognizable if it is the complement of a Turing-recognizable language
Relationship between languages
Some variants
The original model and reasonable variants (e.g. finite amount of work/step)
have same computational power. The following are all equivalent to the original model:
| Machine | Description |
|---|---|
| stay | machine does not have to move left or right at each step, can stay in place: \(\delta: Q \times \Gamma \rightarrow Q \times \Gamma \times \{L, R, S\}\) |
| multitape | multiple tapes and each tape has own read/write head which move simultaneously, initial input is on tape 1 |
| nondeterministic | at each step the computation may proceed according to several possibilities: \(\delta: Q \times \Gamma \rightarrow \mathcal{P}(Q \times \Gamma \times \{L, R\})\) |
| enumerator | machine with an attached printer for producing output; the enumerated language is the strings eventually printed by the machine |
Other unequal alternative models:
-
Linear bounded automaton (LBA)
- restricted TM where the head is not allowed to move off the portion of tape containing input; attempt to move outside the tape causes the head to stay
- LBA can decide every CFL; some decidable languages cannot be decided by LBA
-
Oracle Turing machine
- modified Turing machine that has the additional capability of querying an oracle
- oracle is an external device that is capable of reporting whether any string w is a member of language L
- can decide more languages than an ordinary Turing machine can