13. Algorithm X

Feb 24, 2021

Crash & Restart

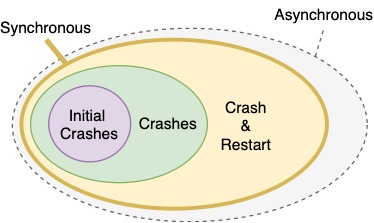
When using a failure model where processors are allowed to restart: 1. where do they restart? - If there is a clock, processor can synchronize with others; otherwise will need to restart work from the beginning 2. what is the state of memory? - Can the processor resume state or is everything lost?

self-stabilization - when processor cannot rely on any information except compile time constants

Asynchronous crash model - when crash & restart occurs with memory - also when arbitrary delays occur in the environment (same as "restart")

Synchronous Crash & Restart

Consider synchronous crash & restart, synchronous model without memory loss, and algorithm W.
If synchronized clock exists, wait for the start of next block step, then jump back in.
If the adversary crashes all but one processor during enumeration, then restarts them, there are \(P-1\) restarts:
- work complexity becomes \(P \cdot N \cdot \log N\)
- BUT we can run Algorithm W without enumeration
With crashes, work complexity is (a function of) \(W = (f, N, P)\)
With restarts, work complexity is (a function of) \(W = (f, r, N, P)\)
Charge \(\Theta(r \cdot \log N)\) work for waiting for restarts:
\(O(N (P-1) \lg N)\)

Algorithm V: \(W = O(N + \lg N + r \cdot \lg N) = N + P(\frac{\lg^2 N}{\lg \lg N})\)

We want \(P(\lg^2 N)\) to be comparable to \(r \lg N\) so algorithm doesn't get worse with restarts → \(r \leq P \lg N\)

Asynchronous Crash & Restart

Consider a case with crashes and restarts

local time is meaningless
enumeration becomes meaningless
can load balance with progress trees

Consider the following node with 2 children:

.   M      # M - parent
  /   \    # L - left child
 L     R   # R - right child

Cannot perform M = L + R in asynchrony. In machine code we would need to perform:

load L
load R
add L, R
write

which is not an atomic sequence. If \(P\) falls asleep before write and another processor makes progress, the write will undo that progress (this phenomenon is called globber).

The problem is that the computation is not monotone → key to dealing with these issues is keeping important data structures monotonistic (so they only increase).

In real systems some hardware use bus interlocking to create atomic sequences → this is a performance killer; use only sparingly and not in massively parallel systems.

Using Booleans

Here is the idea:

.   M      # if L == 1 && R == 1 then M = 1
  /   \
 L     R

The machine sequence for this is:

load L
load R
compare 1
compare 1
if 0 jump;
M := 1

In this example false is never written

when ready to write it does not matter if processor is delayed
this is a monotone

Issue: if you find 0 at tree height, then you know nothing about progress and have to search the tree. This will require more complicated load balancing.

Determining next action

Processor wakes up somewhere in a tree, then evaluates its children:

if both are 1, set parent to 1 and go up the tree
if one child is marked done, go down the other, undone path
if processor is at a leaf: do the work, then write 1 at the leaf (or if already done, do nothing), then go up
if both children are 0, options:
- OPTION 1: can use probability to send processors down varying paths
  - this is not ideal in the worst case
- OPTION 2: use source routing to resolve 0 - 0 case

Algorithm X

while root != 1
    case a: if L == 1 && R == 1
        then M = 1, go up
    case b: if L == 1 && R == 0
        then go right
    case c: if L == 0 && R == 1
        then go left
    case d: if at leaf
        then do work
    case e: if L == 0 && R == 0
        then at level h of tree:
            if PID_binary = [h] == 0
                then go left
                else go right
end while

Binary tree with two sides

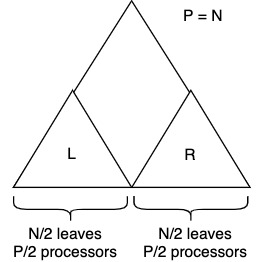
Left or right side of the tree will finish first

\(W_{N, P} = W_L + W_R\)

Let's assume left side finishes first, then:

\(W_{N,P} = W_{\frac{N}{2}, \frac{P}{2}} + W_R\)

Next processors migrate to right side of the tree.

\(W_{N,P} = W_{\frac{N}{2}, \frac{P}{2}} + W_{\frac{N}{2},P}\)

All processors have a doppelganger, and work becomes:

\[ W_{N,P} = W_{\frac{N}{2}, \frac{P}{2}} + 2 \cdot W_{\frac{N}{2},P} \\ \]

\[ = 3(W_{\frac{N}{2}, \frac{P}{2}}) \]

\[ = 3 \cdot 3 (W_{\frac{N}{4}, \frac{P}{4}}) \]

\[ = 3 \cdot 3 \cdot 3 (W_{\frac{N}{8}, \frac{P}{8}}) \]

\[ \vdots \]

\[ = 3^k \cdot (W_{\frac{N}{2^k}, \frac{P}{2^k}}) \]

Notice the recurrence. It will be done when \(2^k = N\) or \(k = \log_2 N\) (do not lose log base!); and \(W_{1,1} = \Theta(1)\)

\[ 3^k \cdot (W_{\frac{N}{2^k}, \frac{P}{2^k}}) = O(3^{\lg_{2}N} \cdot \Theta(1)) \]

Work for 1 processor, per task \(O(3^{\lg_{2}N}) = O(N^{\lg_{2}3})\). \(\lg_23 \approx 1.59\) and we get \(O(N^{1.59})\). Is this good? Yes, it is polynomially efficient. Asymptotically it is and between \(N\ lg N\) and \(N^2\) which is the range we want.