Skip to content

8. Parallel Prefix

Feb 8, 2021

Parallel Prefix

  • Given \(P = 4\), \(N = 12\)
  • \(N\) is approximately 16 and \(\log N \approx 4\)
\[ P = \frac{N}{\lg N} \approx \frac{16}{4} = 4 \]
\[ \text{Chunk} = \frac{N}{P} = \frac{12}{4} = 3 \]

Phase 1: perform summation then store result in leaves

Phase 2: do prefix sum: add left sibling

img

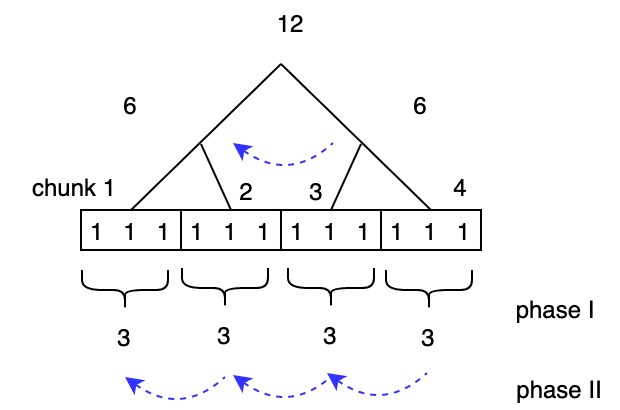
Phase 3: do uniprocessor prefix on chunks: \(S_i = S_{i+1} + X_i\) (add offset from previous chunk)

img

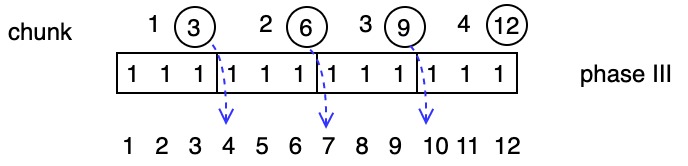
Phase 1 gives optimality, phase 2 gives speed, and phase 3 preserves optimality.

Bounds
\(N/P\) phase I
\(\lg P\) phase II
\(N/P\) phase III
\(\Theta(N/P + \lg P)\) time
\(\Theta(N + P \lg P)\) work

Work is optimal when \(W = N\):

\[ P \lg P \leq N \\ = P \leq N / \lg N \]

Alternative strategy: do prefix sum in phase I. In phase III add left neighbor (not sibling) to each value.

Compaction

Applications of prefix sum include: 1. processor enumeration 2. compaction: "filter a subset from a larger set" or compacts a distributed array over large range to a compact array

Example 1: Find students

Given array \(A\) of \(N\) students, find all that earned A gpa last semester.

Step 1. process \(A\) and select eligible students. If eligible store 1 at leaf, else store 0.

Step 2. run parallel prefix

Step 3. run compaction. If eligible then B[e] = student_id.

1
2
3
4
5
6
7
Array A: [ | | | | | | | ]

 Step 1: [0|1|1|0|1|1|1|0]

 Step 2: [0|1|2|2|3|4|5|5]

 Step 3: [1|2|3|4|5]

5 eligible students remain in array \(B\) after compaction.

Example 2: Categorization

Categorize students by letter grade:

Step Explanation Time
1 Compact A \(\lg N\)
2 Compact B \(\lg N\)
3 Compact C \(\lg N\)
4 Compact D \(\lg N\)
5 Compact F \(\lg N\)

Overall time: \(T_p = \Theta(k \cdot \lg N)\) (for this example \(k = 5\)) Work: \(P \cdot T_P = \Theta(k \cdot N \lg N)\)

You can make this faster by looking only at 0 indices after each pass. Everything with 1 has already been processed previously (local optimization).

Notes on sorting

  • Lower bound of comparison sort is \(\Omega(N \lg N)\): for an array of N items, there are \(N!\) permutations
  • Upper bound is \(O(N \lg N)\)

When does \(W_P = \Theta(k \cdot N \lg N) \leq T_{1}^{*} = O(N \lg N)\)?

If \(k\) is a constant optimal \(W_P\) may exist such that \(W_P = T_{1}^{*}\).

(Are we using comparison sort here? No.)

Radix sort has different bounds: use it when \(k\) is small or \(k \ll N\) (when there are modest number of sort cases).

Zero Before Use

In PRAM world we have shared memory where memory is initialized to 0s. Now enumerate the processors:

  1. Processors that are present set their leaves to 1 then sum up the tree
  2. Only processors \({3,4,5}\) are preset and tree is dirty — how to do this?

img

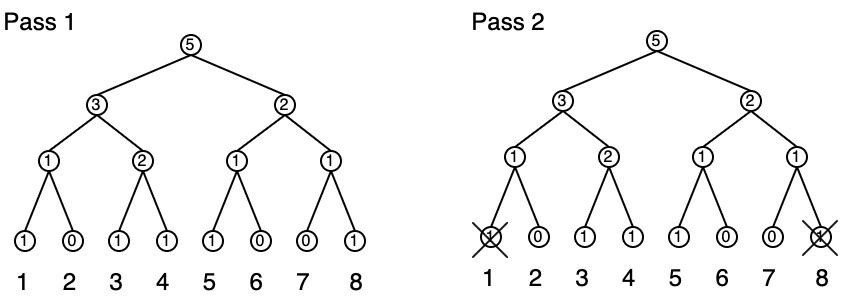
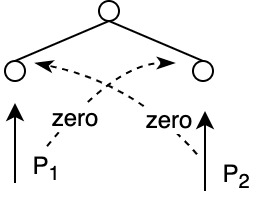
Zero before use: assume neighbor is dead. Zero the parent of the neighbor. Then each processor sets themselves to 1. The cost of zeroing is constant: 1 operation / leaf / processor.

Memory Bootstrapping technique

Assume \(P=N\) and that memory is garbage

Step 1. all processors clear 1 location

Step 2. use 1 processor to clear \(\lg N\) locations

Step 3. use \(\lg N\) processors to clear \(\lg^2N\) locations

... continue until everything is clear, \(\lg^q(N) = N\).