Basics

Summarized notes from Introduction to Data Mining (Int'l ed), Chapter 5

• Basic clustering problem

  • given: set of objects \(X\), inter-object distances \(D(x,y) = D(y,x) \enspace x,y \in X\)
  • output: partition \(P_D(x) = P_D(y)\) if \(x,y\) are in the same cluster

• divide data into meaningful and/or useful groups, to describe or summarize data

  • clusters describe data instances with similar characteristics
  • ideally: small distance between points in cluster; long distance between clusters

• Some utility applications: data summarization, compression, efficiency in finding nearest neighbors

• clustering problem is very much driven by specific choice of algorithm

Clustering techniques

• based on nesting of clusters:

  • partitional (un-nested): divides data into non-overlapping clusters such that each instance is in exactly one cluster
  • hierarchical (nested): clusters are permitted to have sub-clusters; can be visualized as a tree

• based on count of instance memberships:

  • exclusive: each instance belongs to a single cluster
  • overlapping / non-exclusive: instance can belong to more than one cluster
  • fuzzy / soft: (probabilistic) instances membership in each cluster is determined by weigh 0-1, and typical additional constrain requires sum of weights equal to 1 => convert fuzzy to exclusive by assigning each object to cluster with highest weight

• based on instance membership in any cluster:

  • complete: each instance is assigned to some cluster
  • partial: not all instances are assigned a cluster; primary motivations include omitting noise and outliers

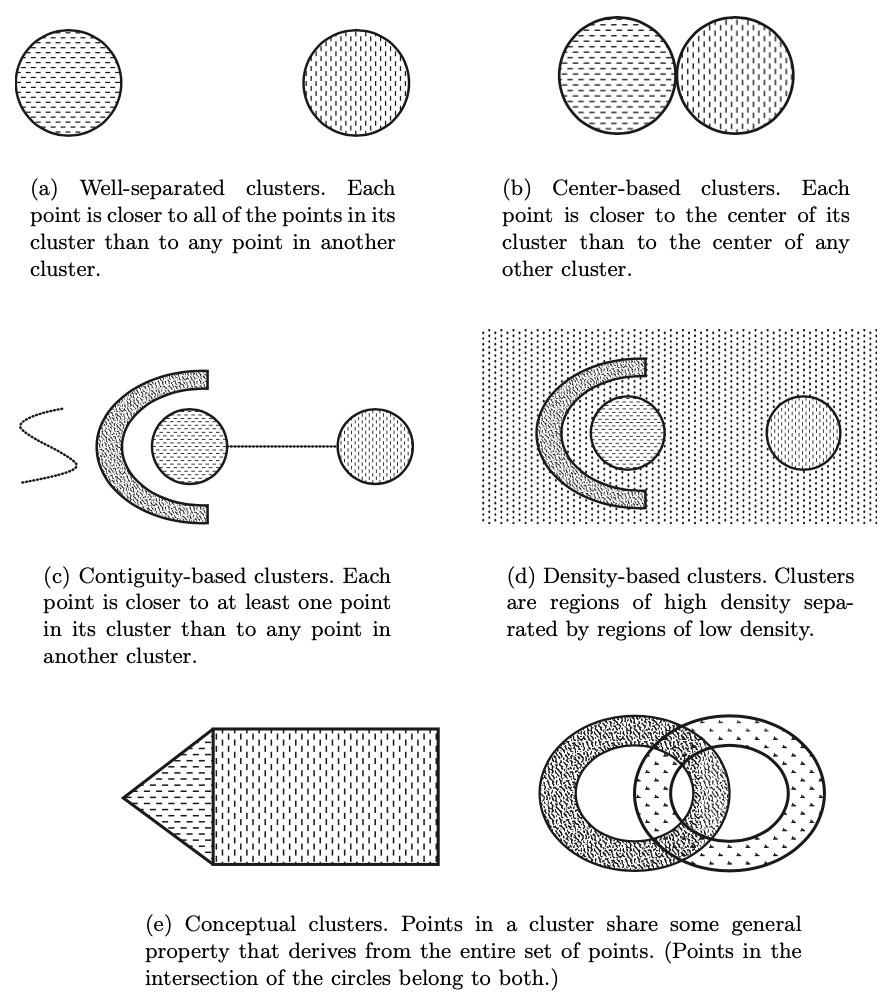
Types of clusters

• well-separated: the distance between clusters is larger than distance between any two points within a cluster

• prototype-based / center-based: prototype defines a cluster and each object in cluster is closer to prototype that defines the cluster than to prototype of any other cluster; the prototype may be actual record or the calculated centroid

• contiguity-based / nearest neighbor / transitive: each point in a cluster is closer (or more similar) to one or more other points in the cluster than to any point not in the cluster.

• graph-based: nodes represent data objects, and edges their connections; cluster is a connected component where each node is connected within cluster but there are no connections to outside the cluster => when nodes are strongly connected, then the nodes form a clique

• density-based: cluster is dense region surrounded by a region of low density => useful strategy when clusters are irregular, intertwined or when noise or outliers are present

• shared-property/conceptual clusters: objects in a cluster share some common property; this encompasses all of the above, but enables defining clusters not covered by previous definitions.

Clustering properties

• Richness: for any assignment of objects to clusters there is some distance matrix \(D\) such that \(P_D\) returns that clustering \(\forall C \enspace \exists D \enspace P_D = C\)

• Scale-invariance: scaling distances by a positive value does not change the clustering \(\forall D \enspace \forall_{K>0} \enspace P_D = P_{KD}\)

• Consistency: shrinking intra-cluster distances and expanding inter-cluster distance does not change the clustering \(P_D = P_{D'}\)

Impossibility theorem: no clustering algorithm can have all 3 properties.

Other considerations:

• order dependence: whether results differ based on the order of processing of data points
• nondeterminism: whether different runs give different results
• scalability: how large datasets the clustering algorithm can reasonably handle
• parameter selection: number of parameters and selection of optimal parameter values

Algorithms

Algorithm	Description	Category	Time Complexity (optimal)	Space Complexity
K-means	Find \(K\) clusters represented by centroids	prototype-based, partitional, complete	\(O(IKmn)\)	\(O((m + K) n)\)
Agglomerative hierarchical clustering	Find hierarchical clusters by merging clusters	prototype-based / graph-based, hierarchical, complete	\(O(m^2 \lg(m))\)	\(O(m^2)\)
DBSCAN	Cluster by density, ignoring low-density regions	Density-based, partitional, partial	\(O(m \log m)\)	\(O(m)\)
Fuzzy C-means	Points have weighted membership in clusters	prototype-based, partitional, fuzzy	\(O(LKI)\)	\(O(LK)\)

where: \(m\) = number of points (records); \(n\) = number of attributes; \(I\) = number of iterations until convergence; \(K\) = number of clusters, \(L\) is the number of links

Also see:

• Expectation Maximization - statistical approach using mixture models
• Single-linkage clustering (SLC) - special case of agglomerative using single-link
• Self-organizing maps - clustering and data visualization based on neural networks

Cluster Validation

Some considerations:

• clustering tendency - distinguishing if non-random structure actually exists in the data
• determining correct number of clusters
• Evaluating how well the results of a cluster analysis fit the data without reference to external information.
• Comparing the results of a cluster analysis to externally known results, such as externally provided class labels.
• Comparing two sets of clusters to determine which is better

Defining cluster evaluation metrics is difficult, there are 3 general categories:

1. unsupervised: measure goodness without reference to external information (e.g. SSE); two subclasses:

   • cohesion: compactness, tightness - how closely related objects in a cluster are
   • separation: isolation - how distinct or well-separated clusters are

2. supervised: measures the extent to which the clustering structure discovered by a clustering algorithm matches some external structure (e.g. entropy of class labels compared to known class labels)

3. relative: Compares different clusterings or clusters, using either supervised or unsupervised metrics

Unsupervised

Cohesion and separation

• for graph-based view of cohesion/separation:

  • \(\displaystyle \text{cohesion}(C_i)\) = \(\sum_{x \in C_i, y \in C_i} proximity(x, y)\)
  • \(\displaystyle \text{separation}(C_i, C_j)\) = \(\sum_{x \in C_i, y \in C_j} proximity(x, y)\)

• proximity function can be similarity or dissimilarity

• If clusters have prototype (centroid or menoid)

  • cohesion and separation can be defined as distance from prototype:
    \(\displaystyle \text{cluster SSE}\) = \(\sum_i \sum_{x \in C_i} distance(c_i, x)^2\)

  • Group sum of squares (SSB) measures distance between clusters
    \(\displaystyle \text{Total SSB}\) = \(\sum_{i=1}^{K} m_i \times distance(c_i, c)^2\)

The result of cohesion/separation can be used to improve clustering by merging or splitting clusters

Silhouette Coefficient

• Evaluation metric for evaluating points in a cluster. Steps:

  • Calculate \(a_i\), which is the average distance from object \(i\) to all other objects in its cluster

  • Calculate \(b_i\), which is the minimum average distance from object \(i\) and objects in any cluster not containing \(i\)

  • The silhouette coefficient is: \(s_i = (b_i - a_i)/max(a_i, b_i)\)

• The range of coefficient is -1 to 1. Negative value is bad; as high as possible is good (obtained when \(a_i=0\)).

• Cluster S.C. can be computed by taking the average S.C. of its points
• Does not work well on arbitrary shapes.

Cophenetic Correlation Coefficient (CPCC)

Cophenetic Correlation Coefficient (CPCC) metric is for evaluating hierarchical clustering

• cophenetic distance between two objects is the proximity at which an agglomerative hierarchical clustering technique puts the objects in the same cluster for the first time
• CPCC calculates the difference between cophenetic distance and original distance matrix

Supervised

• supervised methods include knowing the real cluster data labels
• can help establish "ground truth" for clustering results
• similar metrics can be defined for precision, recall and F-measure

Entropy

• measure the degree of clusters matching known class labels

• For a set of clusters, \(e\):

  \(\displaystyle e = \sum_{i=1}^{K} \frac{m_i}{m} e_i\)

• For individual cluster, \(e_i\):

  \(\displaystyle e_i = -\sum_{j=1}^{L} p_{ij} \lg p_{ij}\)

  where:

  • \(L\) is number of classes
  • \(p_{ij} = m_{ij}/m_i\)
  • \(m_i\) is number of objects in cluster \(i\)
  • \(m_{ij}\) is number of objects of class \(j\) in cluster \(i\)

Purity

• the maximum \(p_{ij}\) for a cluster

• overall purity of a cluster is

  \(\displaystyle \sum_{i=1}^{K} \frac{m_i}{m} max_j(p_{ij})\)