24. NP-Reductions

Apr 12, 2022

Recall theorem: if language A is NP-complete, language B is in NP, and A is polynomially reducible to B, then B is NP-complete.

Using the previous theorem, prove that the following problems are NP-complete.

Vertex Cover

Vertex cover of a graph is a subset of nodes S such that every edge in the graph touches at least one node in S, see vertex cover ↗.

• Size of vertex-cover is the number of nodes in the cover, \(|S|\).

• Corresponding language

  VERTEX-COVER = \(\{\) \(<\) \(G,k\) \(>\): graph \(G\) contains vertex cover of size \(k\) \(\}\)

Theorem. VERTEX-COVER is NP-complete.

Proof.

1. VERTEX-COVER is in NP can be easily proven.

2. We will reduce in P-time 3CNF-SAT to VERTEX-COVER (NP-complete)

Let \(\phi\) be a 3CNF formula with \(m\) variables and \(l\) clauses.

e.g. \(l = 3, m = 4\)

\[ \phi = (x_1 \lor x_2 \lor x_3) \land (\overline{x_1} \lor \overline{x_2} \lor \overline{x_4}) \land (\overline{x_1} \lor x_3 \lor x_4) \]

Formula \(\phi\) can be converted to a graph \(G\) such that: \(\phi\) is satisfied \(\Leftrightarrow\) \(G\) contains vertex cover of size \(k=m+2l\).

Construct gadgets:

size 2 (2m nodes), variable gadgets

x1 -- !x1       x2 -- !x2       x3 -- !x3      x4 -- !x4


size 3: (3l nodes), clause gadgets

     x1                 !x1                 !x1
    /  \               /   \               /   \
  x2----x3           !x2---!x4           !x3---x4  

Link the literals between variable and clause gadgets

     x1 ------ !x1       x2 -- !x2       x3 ---  !x3      x4 -- !x4
     |          |\       |      |         |       |       |      |
     |   |------|-\------|------|---------|       |       |      |
  |--|---|------|--\-----|   |--|-----------------|-------|------|
  |  |   |      |   \        |  |         |-------|       |
  |  x1  |      |    !x1     |  |   |-----|-!x1           |
  | /  \ |      |   /   \    |  |   |     | /  \          |
  x2----x3      | !x2---!x4--|  |   |    !x3---x4---------|  
                |  |------------|   |            
                |-------------------|     

1. \(\phi\) is satisfied \(\Rightarrow\) \(G\) contains vertex cover of size \(k=m+2l\).

Choose values for each variable \(x_1,...x_i\). Put every satisfying literal in the cover (in variable gadgets). Then select one satisfying literal in each clause gadget and include the remaining literals in the cover. There is a vertex cover since every edge is adjacent to a chosen node.

    (x1) ------ *        * -- (!x2)       * --- (!x3)    (x4) -- *
     |          |\       |      |         |       |       |      |
     |   |------|-\------|------|---------|       |       |      |
  |--|---|------|--\-----|   |--|-----------------|-------|------|
  |  |   |      |   \        |  |         |-------|       |
  |  *   |      |   (!x1)    |  |   |-----|(!x1)          |
  | /  \ |      |   /   \    |  |   |     | /  \          |
 (x2)---(x3)    |  *--(!x4)--|  |   |     *---(x4)--------|  
                |  |------------|   |            
                |-------------------|     

( )  == selected     * = not selected       

In general case:

• edges in variable gadgets are incident to at least one node in the cover.
• edges in clause gadgets are incident to at least one node in the cover, since two nodes are chosen in a clause gadget

Every edge connecting variable gadgets and clause gadgets is one of three types (1 node in variable is selected, 1 node is clause gadget is selected, or both are selected). The case where neither is selected cannot occur by the rules of this construction.

1. \(G\) contains vertex cover of size \(k=m+2l\) \(\Rightarrow\) \(\phi\) is satisfied.

2. exactly one literal in each variable gadget is chosen

3. exactly two nodes in each clause gadget is chosen

For 3CNF variable assignment, choose the literals is the cover from variable gadgets, e.g.

\[ x_1 = 1, x_2 = 0, x_3 = 0, x_4 = 1 \]

3CNF-SAT \(\phi\) is satified since the respective literals satisfy the clauses:

\[ \phi = (x_1 \lor x_2 \lor x_3) \land (\overline{x_1} \lor \overline{x_2} \lor \overline{x_4}) \land (\overline{x_1} \lor x_3 \lor x_4) \]

The proof can be generalized for arbitrary \(\phi\). The graph \(G\) is constructed in polynomial time with respect to the size of \(\phi\). Therefore, we have reduced in polynomial time 3CNF-SAT to VERTEX_COVER.

Hamiltonian path

Theorem. HAMILTONIAN-PATH is NP-complete.

Proof.

1. HAMILTONIAN-PATH is in NP - can be easily proven.

2. We will reduce in P-time 3CNF-SAT to HAMILTONIAN-PATH (NP-complete)

Consider arbitrary CNF formula: \((x_1 \lor x_2) \land (\overline{x_1} \lor x_2)\), but the following applies to 3CNF formulas as well.

Build a diamond-structure gadget fot variable \(x_1\). Number of nodes in a row is \(3l+3\) for \(l\) clauses.

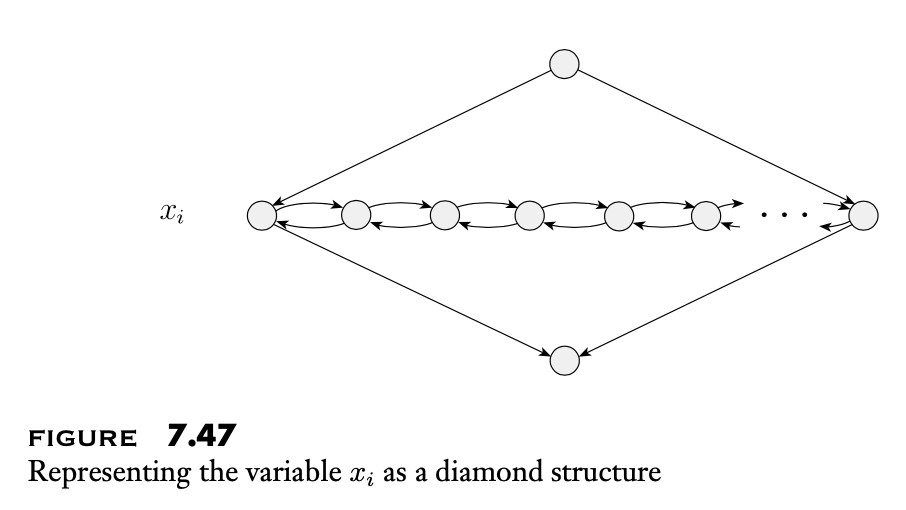
A pair of nodes in gadget for each clause node. Pairs separated by a node.

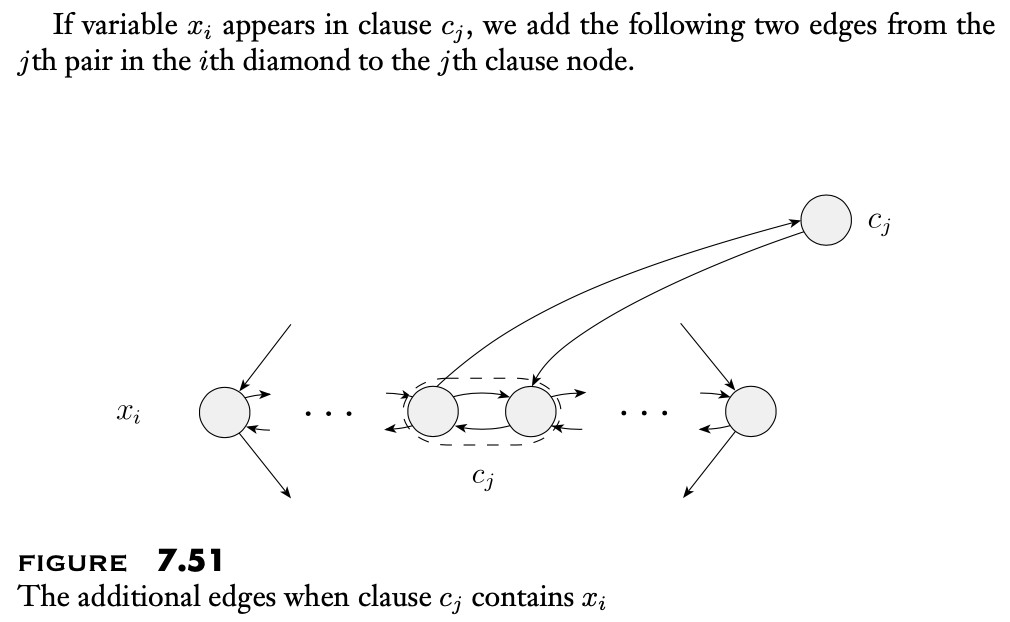
• if variable appears as-is in clause: first edge from gadget outgoing (left to right), second edge from gadget is incoming.
• if variable appears inverted in clause: first edge from gadget incoming (left to right), second edge from gadget outgoing.

Combine the gadgets to form a complete graph.

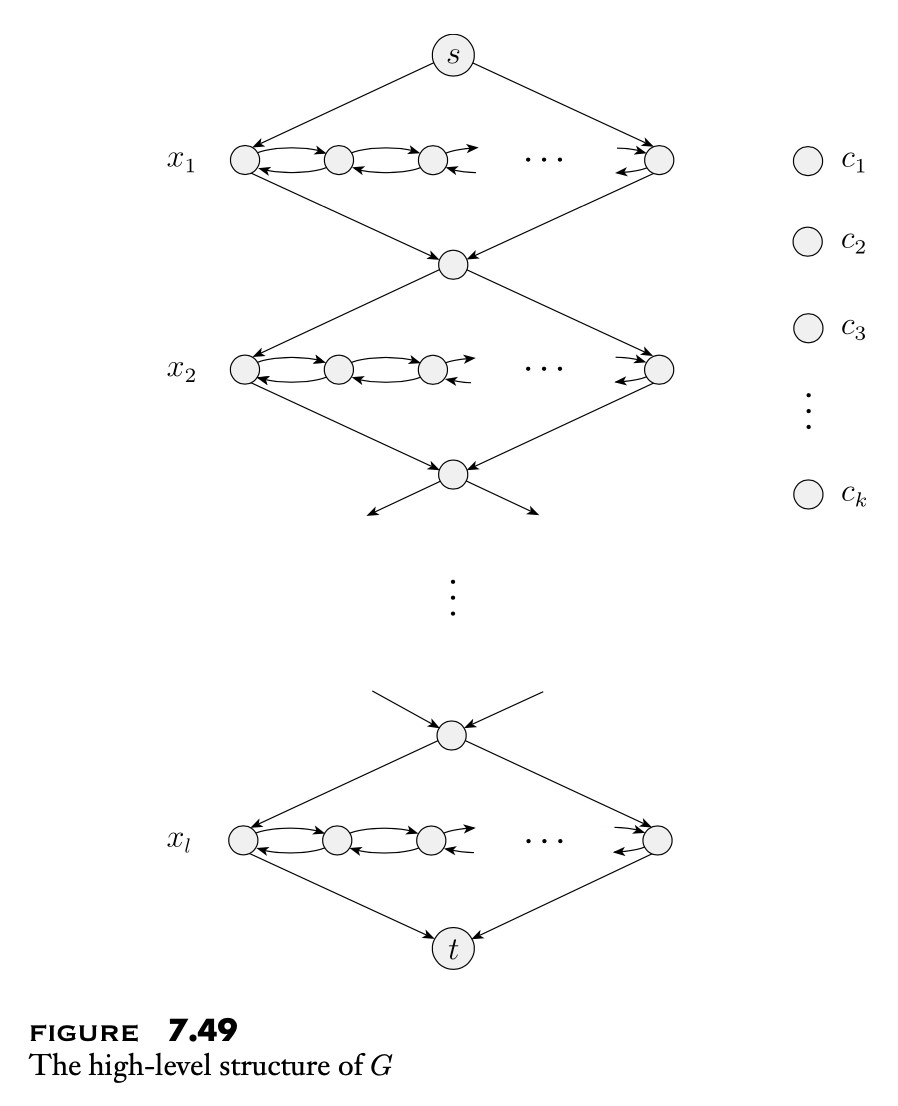
• If variable is set to 1, traverse its gadget from left to right.
• Visit clauses satisfied from the variable assignment.
• for each clause pick one variable that satisfies it and visit respective node once from that variable gadget

Symmetrically it can be shown: if the graph has a Hamiltonian path, then the formula has a satisfying assignment.

Basic idea: each clause node is visited exactly once from some variable gadget, and that variable satisfies the clause. It is impossible a clause node to be traversed from different variable gadgets.

Therefore the formula is satisfied iff the respective graph has a Hamiltonian path. The proof can apply to any 3CNF formula. The graph is constructed in polynomial time with respect to the size of the formula.

Therefore we have reduced in polynomial time 3CNF-SAT to HAMILTONIAN-PATH.