23. NP-Complete
Mar 29/31, 2022
Polynomial time reductions
Polynomial computable function \(f\): there exists a Turing machine \(M\) such that for any string \(w\) computes \(f(w)\) in polynomial tine \(O(|w|^k)\).
Observation: the length of \(f(w)\) is bounded \(|f(w)| = O(|w|^k)\), since \(M\) cannot use more than \(O(|w|^k)\) tape space in time \(O(|w|^k)\).
Definition. Language A is polynomial time reducible to language B if there is a polynomial computable function \(f\) such that \(w \in a \Leftrightarrow f(w) \in B\).
Theorem. Suppose that \(A\) is polynomial time reducible to \(B\). If \(B \in P\) then \(A \in P\).
Proof. Let \(M\) be the machine that decides B in polynomial time. Construct machine \(M^{'}\) to decide \(A\) in polynomial time. On input string \(w\):
- Compute \(f(w)\)
- Run \(M\) on input \(f(w)\)
- If \(f(w) \in B\) then accept \(w\).
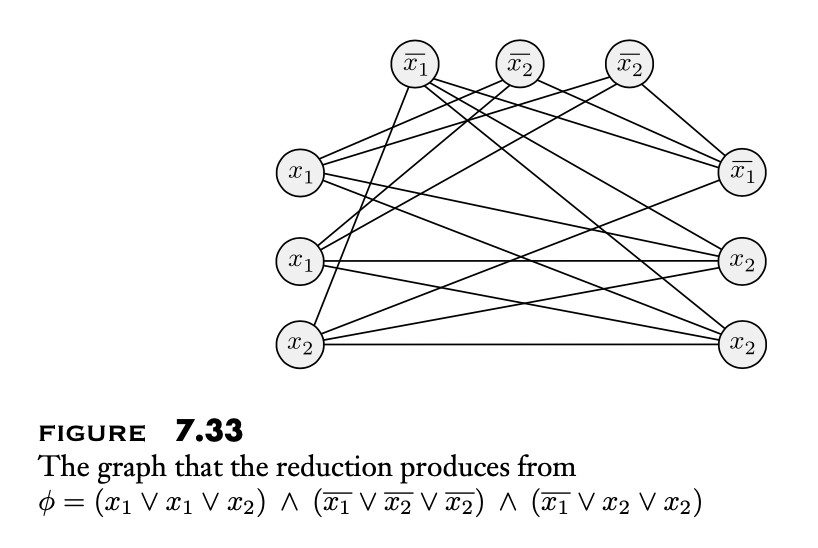
Reducing 3CNF to CLIQUE
3CNF
- each clause has 3 literals e.g. \((x_1 \lor \overline{x_2} \lor \overline{x_3}) \land (x_3 \lor \overline{x_5} \lor x_6) \land \dots\)
- language: 3CNF-SAT = { \(w\) : \(w\) is a satisfiable 3CNF formula }
Clique
- Language: CLIQUE = { \(<\) \(G,k\) \(>\): graph \(G\) contains a \(k\)-clique }
Theorem: 3CNF-SAT is P-time reducible to CLIQUE
Proof. give a polynomial time reduction of one problem to another.
Transform formula to graph: if formula is satisfied, graph will have k-size clique \(\Leftrightarrow\) is graph has \(k\)-size clique, then formula is satisfiable. Steps:
- for each 3CNF clause, create a node for each of its variables
- Add a link from a literal \(l\) to a literal in every other clause, except its complement \(\overline{l}\)
- The formula is satisfied iff the graph has a k-clique
NP-Complete languages
We define the class of NP-complete languages:
╭——————————————————————╮ │ Decidable │ │ ╭—————————————————╮ │ │ │ NP │ │ │ │ ╭—————————————╮ │ │ │ │ │ NP-Complete │ │ │ │ │ ╰—————————————╯ │ │ │ ╰—————————————————╯ │ ╰——————————————————————╯
Every problem in NP can be transformed in P time to any NP-complete problem, i.e. a language \(L\) is NP-complete if: (1) L is in NP and (2) every language in NP is reduced to L in P-time. If a NP-complete language is proven to be in P, then P=NP.
Theorem. If language \(A\) is NP-complete, and language \(B\) is in NP, and \(A\) is polynomial time reducible to \(B\) => then \(B\) is NP-complete.
Proof. Any language \(L\) in NP is polynomial time reducible to \(A\). Thus \(L\) is polynomial time reducible to \(B\).
Cook-Levin Theorem
Language SAT (satisfiability problem) is NP-complete.
Proof. Part 1: SAT is in NP (proven previously). Part 2: reduce all NP languages to the SAT problem in polynomial time.
Take an arbitrary language \(L \in NP\). We will give a P-time reduction of \(L\) to SAT. Let \(M\) be nondeterministic TM that decides L in P-time.
Provable by construction: for any string \(w\), we can construct in P-time a Boolean expression \(\phi(M,w)\) such that \(w \in L \Leftrightarrow \phi(M,w)\) is satisfiable.
-
SAT is free-form Boolean expression
-
CNF (conjunctive normal form) contains clauses of Boolean expressions
- 3CNF is case of exactly 3 literals in each clause
- CNF form can be converted to 3CNF in P time
-
SAT, CNF-SAT, 3CNF-SAT are NP-complete languages => known as NP-languages