Skip to content

DBSCAN

Summarized notes from Introduction to Data Mining (Int'l ed), Chapter 5, section 4

Unsupervised learning > clustering

  • density-based clustering located regions of high density, separated from others by regions of low density

  • DBSCAN is based on center-based approach: count number of points within radius, of a selected central point

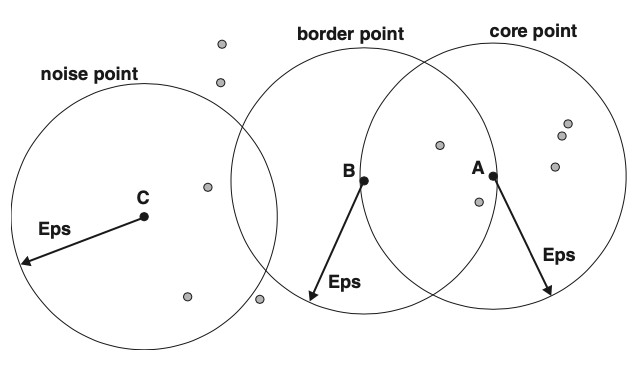
  • Data points are classified in 3 categories:

    • core points: inside the interior of density-based cluster; point is a core point if there are at least \(MinPts\) within specified distance, \(Eps\)

    • border-points: non-core points within the neighborhood of core point; border point can be inside the neighborhood of several core points

    • noise points: points that are neither core or border points

  • DBSCAN produces partial clustering solution

Categories of points

points

Pseudo code

1
2
3
4
5
6
DBSCAN(min_pts, eps):
    label each point as core border, or noise
    eliminate noise
    put edge between all core points within distance eps or each other
    make each group of connected core points into a separate cluster
    assign each border point to one the clusters of its associated core points

Choosing parameters

  • For \(MinPts\) typical approach is to look at the behavior of distance of a point to its \(k^{th}\) neighbor

    • for points that belong to cluster, the distance will be small if k is not larger than cluster size

  • compute distance for all data points for some \(k\), sort in increasing order, then plot sorted values

    • distance increases sharply at suitable \(Eps\)
    • use k as \(MinPts\)

  • if \(k\) is too small then even small number of noise points can form a cluster

  • if \(k\) is too large, then small clusters of size < \(k\) will be labelled as noise

  • original DBSCAN used value \(k=4\) which is appropriate for many 2D data sets

Analysis

Complexity

\(m\) - data points \(t\) - time to find points
Time \(O(m \times t)\)
Time, min \(O(m \log m)\)
Time, max \(O(m^2)\)
Space \(O(m)\)

Advantages

  • resistant to noise
  • can handle clusters of varying shapes and sizes => can find clusters not discoverable with K-means

Limitations

  • algorithm will have issues, if cluster densities vary widely

  • high-dimensionallity: difficult to define density for such data

  • computation can become expensive if dimensionality is high