7. Chunking & Prefix
Feb 3, 2021
Padding
- assume \(N\) where \(2^{k-1} < N < 2^k\) (\(N\) is not a power of 2) and \(P = 2^k\)
- then \(2^{k-1} < N < N^{'} < 2^k\) and \(k-1 < \lg N^{'} < k\)
- time: \(T_p = \lg N^{'} = k = \Theta(\lg N)\)
- work: \(W_p = P \cdot \lg N^{'} = \Theta(N \lg N)\)
- for an exact power we have:
- \(T_p = \Theta(\lg N)\) and
- \(W_p = \Theta(N \lg N)\)
- padding to an exact power does not make a difference to complexity
Chunking
- Consider an associative operation where \(P=N\) → only 1/2 of processors need on each height → high slackness
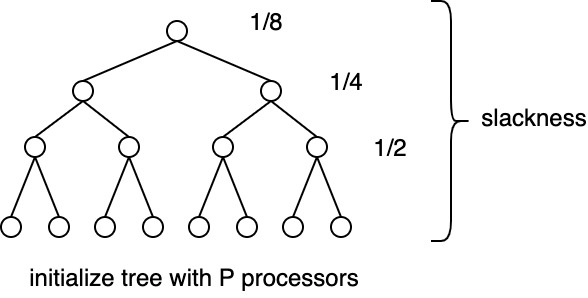
- Next consider a case where \(P \ll N\) (the usual case)
- Perform some associative operation on \(N\) then:
- \(W = \Theta(N \lg N) > \Theta(N) = \Theta(N) = T_1^{*}(N)\)
- when \(P=1\) optimal, not fast
- when \(P=N\) fast, not optimal
- How to be optimal and fast? Give each processor a chunk of \(N/P\) input
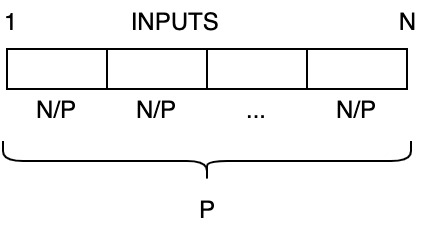
Phase I
- Compute partial sums in leaves
- Time of 1 chunk = \(\Theta(N/P) = T^{(1)}\)
- Work of 1 chunk = \(\Theta(N) = W^{(1)}\)
- So far optimal → now we have \(P\) partial sums in leaves
Phase II
- Add the chunks
- \(T^{(2)} = \Theta(\lg P)\)
- \(W^{(2)} = P \cdot \Theta(\lg P) = \Theta(P \lg P)\)
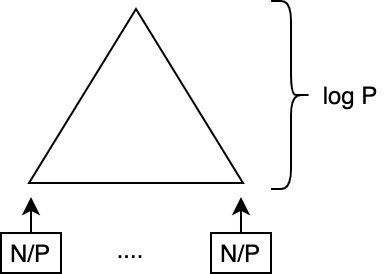
- total time: \(T^{(1)} + T^{(2)} = \Theta(\frac{N}{P} + \lg P)\)
- total work: \(W^{(1)} + W^{(2)} = \Theta(N + P \lg P)\)
- when is \(P \lg P\) optimal? (tree height \(\lt N\))
\[
P \lg P \leq N \\
P \leq \frac{N}{\lg P} \\
P \leq \frac{N}{\lg N} \leq \frac{N}{\lg P} \\
\]
- solve for \(P = N / \lg N\):
- \(1 \leq P \leq N/ \lg N\)
- under these conditions algorithm is optimal
\[
T_{P,N} = \Theta(\frac{N}{N \lg N} + \lg(\frac{N}{\lg N}))
= \Theta(\lg N + (\lg N - \lg \lg N)) \\
\]
\[
= \Theta(2 \lg N - \lg \lg N) \\
= \Theta(\lg N)
\]
\[
W_{P, N} = P \cdot \Theta(\lg N) \\
= \frac{N}{\lg N} \cdot \Theta(\lg N) \\
= \Theta(N)
\]
- Time \(P = \frac{N}{\lg N} \leq \lg N + \lg N = 2 \lg N\)
First strategy to convert a non-optimal algorithm to optimal, is to try chunking
Prefix Computation
- Challenge: compute the sum of \(X[1...N]\) array, such that:
- \(S_1 = X[1]\)
- \(S_2 = X[1] + X[2] = S_1 + X[2]\)
- \(S_3 = X[1] + X[2] + X[3] = S_2 + X[3]\)
- ...
- \(S_k = \sum_{i}^{k}X[i]\)
- ...
- \(S_n = \sum_{i}^{n}X[i]\)
- prefix sum includes self and everything to the left
Uniprocessor implementation
1 2 3 | |
- Time (precise analysis): \(T_1 = 1 + (N-1) \cdot 1 = N\)
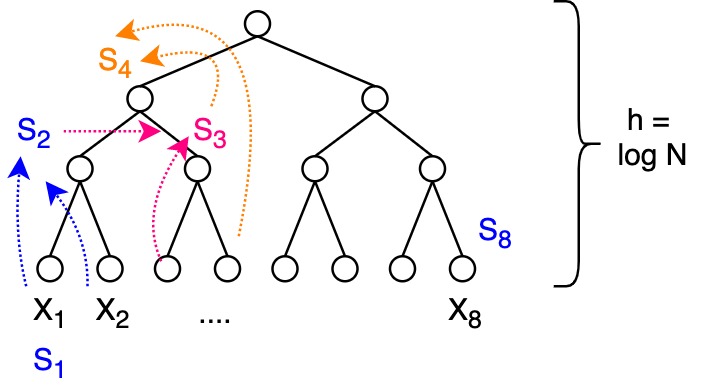
Parallel Prefix
- similar to processor enumeration
- almost all processors work → not similar slackness as with addition
- \(T_p = \Theta(\log N)\)
- \(W = P \cdot T_P = \Theta(N \lg N) > T_1^{*}(N)\)
- Not optimal, but log efficient
Strategy 1: do in 2 passes 1. bottom-to-top summation 2. top-to-bottom add left child
Strategy 2: try chunking - \(P = 1\) slow and optimal, \(P = N\) fast and not optimal → choose chunk size \(\lg N\)
steps: 1. sum chunks: \(T_{(1)} = N/P\) (\(< \lg N\)) 2. compute prefix sum (\(z_{1-4}\)): \(T_{(2)} = \lg P\) (\(< \lg N\)) 3. distribute: \(T_{(3)} = N/P\) (\(< \lg N\))
steps combined: \(T_{(1)} + T_{(2)} + T_{(3)} = 3 \lg N\)
- Total time: \(T_{total} = N/P + \lg P + N/P = \Theta(N/P + \lg P)\)
- Work: \(W = \Theta(P \cdot (N/P) + P \lg P) = \Theta(N + P \lg P)\)
- Optimal \(P\) when \(P = N / \lg N\)
Example: Prefix with Chunks
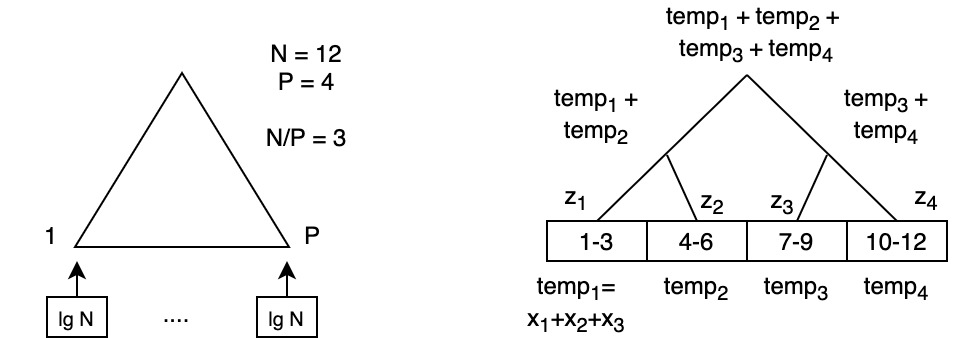
For example, \(P_2\) computes: 1. \(S_4 = X_4 + Z_1\) 2. \(S_5 = X_5 + S_4\) 3. \(S_6 = X_6 + S_5\)
- to compute \(X_4 = X_4 + temp_1\)
- to compute \(X_7 = X_7 + temp_1 + temp_2\)
- before these can be computed, need to know the value to the left