Skip to content

6. DO-ALL

Feb 1, 2021

DO-ALL Problem

Recall PRAM comes with (1) synchrony (2) high bandwidth memory and (3) no failures → now remove synchrony.

In a DO-ALL problem, we have: - \(N\) tasks and tasks are indivisible - \(P\) processors and \(N=P\) - all processors do the same task

1
2
for pid = 1...P do
    DO TASK(PID)

Analysis

Uniprocessor time

\(T_{1,LB}^{*} = \Omega(N)\)     \(T_{1,UB}^{*} = O(N)\)     \(T_1^* = \Theta(N)\)

Parallel time

\(T_P = \Theta(1)\)

\(S = \frac{T_1^*(N)}{T_P(N)} = \frac{\Theta(N)}{\Theta(1)} = \Theta(N) = \Theta(P)\)

\(W = P \cdot T_P(N) = \Theta(P \cdot 1) = \Theta(N) = O(T_1^*(N))\)

When \(W_P = W_{T_1^*}\) work is optimal

Handling asynchrony

One of the biggest problems in parallel computing is distinguishing failed processors from slow processors. If crash occurs then it is detectable.

Fail-Stop processors never perform erroneous state transformation due to failure. Instead, the processor halts and its state is irretrievably lost.

How does asynchrony happen? Can occur from e.g. page faults.

1
2
3
for pid= 1...P pardo
    for i= 1...N
        do task(i)

As long as at least 1 processor does not crash, N tasks will complete; all processors will do \(N\) tasks.

With this strategy: - \(W = P \cdot \Theta(N) = \Theta(N^2)\) → no speedup! - Work lower bound is \(\Omega(N)\)

What we want is to find solutions in this space between \(N\) and \(N^2\):

img


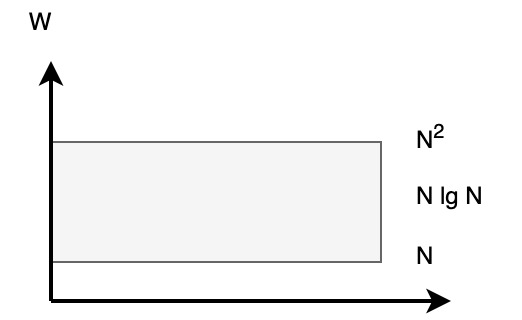
Lower bound for async PRAM DO-ALL is \(\Omega(N \lg N)\). Optimality is not achievable in asynchronous world: the lower bound is \(N \lg N\). No algorithm meets this lower bound.


Algorithms with \(T_P = O(\lg N)\) implies \(W = P \cdot O(\lg N) = O(P \lg N)\). Algorithm is log efficient when the best sequential \(W\) degrades by a log factor.

Oracle vs. Adversary

Goal: finish all tasks.

Challenge: dealing with an adversary who kills processors and tries to slow down progress.

All tasks are: - similar size - idempotent - tasks can be performed repeatedly without harm - independent - order of completion does not matter

Oracle will do perfect load balancing and divide tasks equally between processors.

Adversary kills \(1/2\) of processors on each round.

img


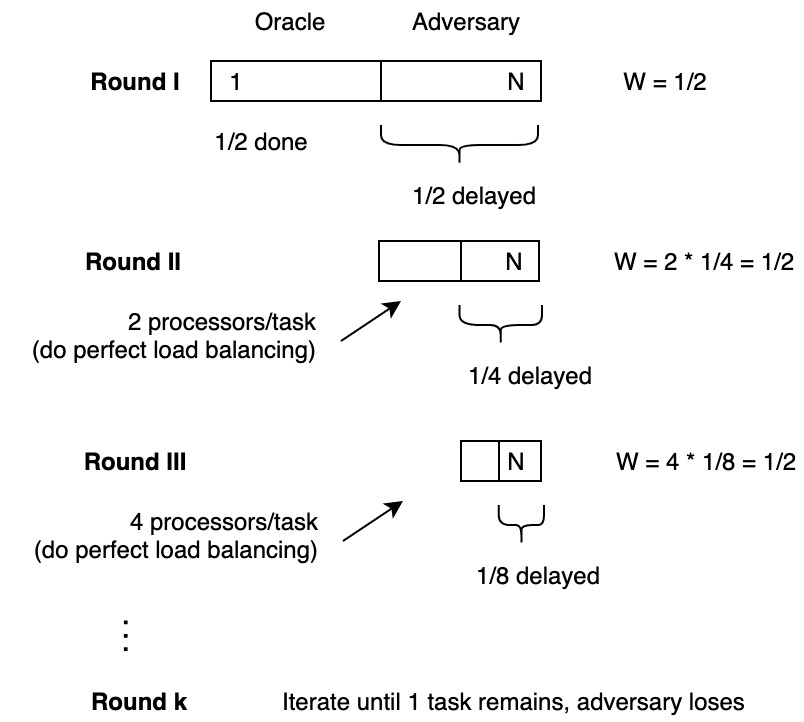
Adversary loses when \(\frac{N}{2^{k-1}} = 1\):   \(N = 2^{k-1}\)     \(\lg N = {k-1}\)     \(k = \Theta(\lg N)\)

Work per round: \(\frac{N}{2} + \frac{N}{2} + \frac{N}{2} + ...\) → \(W = \frac{N}{2} \cdot \Theta(\lg N) = \Theta(N \lg N)\)