24. Omega Networks

Apr 12, 2021

Omega Networks (cont.)

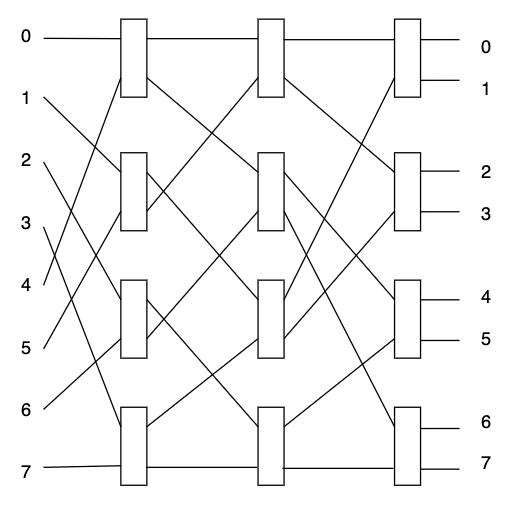
• omega networks built using shuffle exchange
• number of wires/nodes = 4
• Hardware cost $HW\mathrm{\$}=\mathrm{\Theta }(P)+\mathrm{\#}\text{stages}\cdot \text{cost of stage}=P+\log P\times P/2=\mathrm{\Theta }(P\lg P)$
• Latency $<2\cdot \lg P$ ($\log P$ == number of stages)
• Work = $T\cdot HW\mathrm{\$}$
• everything is slowed down a log factor on this hardware
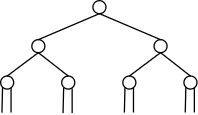
• there are embedded binary trees in the hardware → we can do associative ops in same time as PRAM: $W\cdot \log P$

How to enforce EREW/CREW/CRCW?

• EREW: runtime error if using the same wires
• CRCW: use combining switch that does combining
  • remembers that outgoing message must follow along multiple wires
  • broadcast reads on both output wires

Writes

• common: combine messages, do 1 write
• arbitrary: randomly drop message
• priority: compare sources and drop lower priority message

Not all permutations are possible → can have blocks

• such network is called blocking network
• combining does not help because the carried values may be different
• need higher bandwidth to carry more values

Are there non-blocking networks?

• yes, solution exists for non-blocking networks of depth $\mathrm{\exists }\mathrm{\Theta }(\log P)$
• on practice there exists depth $\mathrm{\Theta }({\lg }^{2}P)$
• simplest: omega network repeated $\log P$ times
• routing of this network gets very complicated and requires an additional controller connected to all stages → controller computes route over $\log P$ stages offline

Pipelining

The logarithmic overhead of omega network does not always apply, e.g.

$z$ sets	$\sum$
1	$\lg P$
2	+1
3	+1

• $HW\mathrm{\$}=T_z=\log P+(z-1)$
• $W=T_z\cdot (P\lg P)<P{\lg }^{2}P+zP\lg P=\mathrm{\Theta }z(P\lg P)$ (amortized)
• make $z>\lg P$ to amortize the $HW\mathrm{\$}$ overhead → good for pipelining

Recirculating Network

Idea is to use one stage to perform as if there were multiple stages.

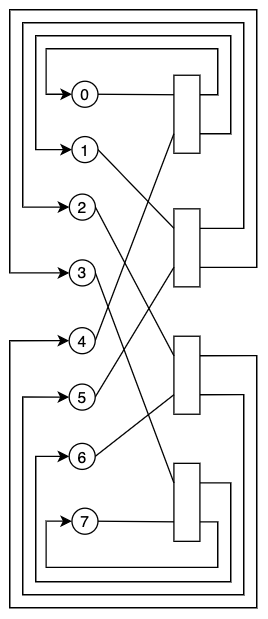
Complications:

• each switch must have a counter to know which action to perform on input; counter is mod $\log P$
• need to store $\log P$ routing info
• pro: $HW\mathrm{\$}$ is now $\mathrm{\Theta }(P)$
• has same blocking issue, cannot pipeline
• this is not a universal hardware → need to know what you are doing when using it!

Prefix sum with omega network

Read 2 inputs, add, send up

$N=8$, $P=7$, $N\approx P$

$P=2L-1=2\cdot \frac{N}{2}-1=\mathrm{\Theta }(N)$

• $T^{(1)}=\mathrm{\Theta }(\lg N)$
• $T^{(2)}=+1$
• $\dots$
• $T^{(7)}=+1$
• $T=\mathrm{\Theta }(\lg N)+2-1$
• $W=\mathrm{\Theta }(N\lg N)+\mathrm{\Theta }(P2)$