22. Cubes
Mar 29, 2021
Measuring Performance
of a message passing system
There are 3 factors to consider:
- (1) message delay = latency
- (2) number of messages
- (3) local computation
Time in a message passing system means = message delay + local computation
- broadcast latency is \(\Theta(N)\)
- delays vary by algorithms (measured as \(d\)), e.g.
- ABD performs 1 round communications (2 delays/round)
- ERATO takes 1.5 rounds (3 delays/round)

Architectures Comparison
- \(W_{PRAM} = P \cdot T_P\)
- \(W_{SIM} = P \cdot T_P \cdot L\) where \(L\) is the simulation latency
3D Cube
- overhead: \(\sqrt[3]{P}\)
- HW cost: \(HW\$ = \Theta(P) + \Theta(6P) = \Theta(P)\)
- Latency: \(L = 3 \sqrt[3]{P} - 3\)

| \(d\) | \(L\) | \(HW\$\) | Wires/P | Wires/Total |
|---|---|---|---|---|
| 1 | \(1 \cdot (P-1)\) | P | 2 | \(2P\) |
| 2 | \(2 \cdot (\sqrt{P}-1)\) | P | 4 | \(4P\) |
| 3 | \(3 \cdot (\sqrt[3]{P}-1)\) | P | 6 | \(6P\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(d\) | \(d \cdot (\sqrt[d]{P}-1)\) | P | \(2d\) | \(2d \cdot P\) |
How small can \(\sqrt[d]{P}\) be?
When \(d \to \infty\) then \(L \to 0\)
\(\sqrt[d]{P} - 1 = 1\)
\(\sqrt[d]{P} = 2\)
\(P = 2^2\)
\(d = \log P\)
Must be at least \(\geq 1\).
Hypercube
| d | P | name | |
|---|---|---|---|
| 0 | \(P = 2^0 = 1\) |  |
empty string \(\lambda\) |
| 1 | \(P = 2^1 = 2\) |  |
0 ... 1 |
| 2 | \(P = 2^2 = 4\) | 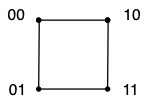 |
00 ... 11 |
| 3 | \(P = 2^3 = 8\) |  |
000 ... 111 |
Any hypercube is a multidimensional grid; not all grids are hypercubes.
Hypercube is logarithmically efficient for simulation:
- great in proctice
- cost in scalability
- number of wires is \(2\log_2P\)
- need to add ports to connect processors
Length of node name is \(| name | = \log_2P\)
Cube-Connected Cycles
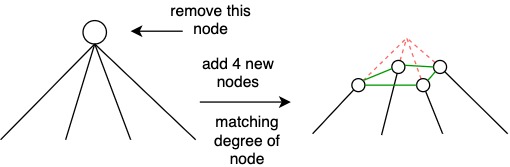
Hypercube of P nodes
- \(P \log P\) nodes and 3 wires/processor
- number of wires is not dependent on P anymore.
This works in other dimensions for hypercubes e.g. 8 node hypercube becomes 24 nodes. Number of wires per processor is 3.
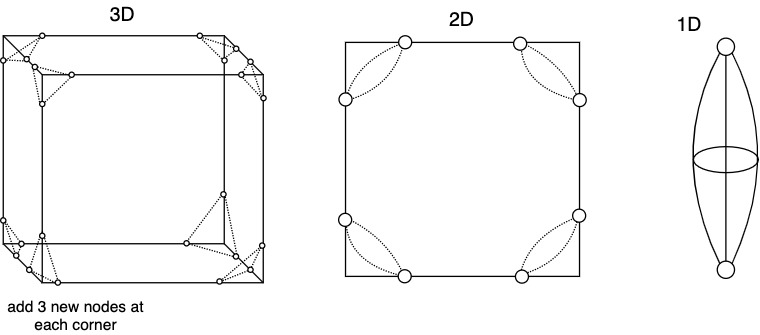
Routing is more complicated now, e.g. routing from 000 to 111
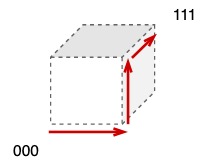
- diameter of graph: max of any distance between two nodes
- diameter of hypercube = \(d\)
- diameter of CCC = \(O(d^2)\)
- \(|name| = \log_2P + \log_2 \log_2P\)