Skip to content

19. Quorums

Mar 17, 2021

Recall transition system modeled using signature, state, transitions \(t_1, t_2, \dots\) where each transition has type NAME (args), a precondition (true/false), and effect: \(s' \leftarrow s\). Actions take place in a sequence: \(s_0, a_1, s_1, a_2, \dots\)

When a transition is a synchronized input actions, the preconditions is true. Server cannot refuse input. In automata, skip the precondition (channel cannot refuse to accept messages). This says nothing about delivery of messages → add a concept of fairness.

Sequence of send actions alone is a valid execution → can reason about liveness after the fact

Use variables to represent phases, e.g.

1
2
3
4
broadcast()   # send.phase = 1
wait
broadcast()   # send.phase = 2
wait

state phase \(\in {1, 2}\) init 1 → enforces good behavior on the client of the service.

well-formedness condition: either applied to automata or the environment and primarily for convenience: exclude behaviors that should not be allowed → does not affect good behaviors in the environment.

Reasoning about atomicity

Recall atomicity: for every execution, there exists a partial order on completed operations such that

  1. if \(\pi_1\) and \(\pi_2\) are operations such that \(\pi_1\) completes before \(\pi_2\), then \(\pi_2 \nprec \pi_1\)
  2. if \(\omega_1\) and \(\omega_2\) are write operations then \(\omega_1 \prec \omega_2\) or \(\omega_2 \prec \omega_1\)
  3. reads are ordered so that \(r_1\) returns value of immediately preceding write or the initial value if there is no such write

Lifecycle or a write:

1
new ts -> broadcast -> wait

Lifecycle of a read:

1
broadcast, wait, choose ts, broadcast, wait

\(\tau\) = timestamp of operation

  • for write: new ts
  • for read: choose ts

partial order (P.O.):

  • \(\omega_1\), \(\omega_2\) then \(\omega_1 \prec \omega_2\) if \(\tau(\omega_1) \prec \tau(\omega_2)\)
  • \(\omega\), \(r\) then \(\omega \prec r\) if \(\tau(\omega) \prec \tau(r)\)

note: writer only does 1 write at a time. Timestamps of writer are monotonic and do not roll back. Can reason about this behavior by observing the code. Timestamps never get lower.

Regarding rule 1 of atomicity, is it possible for the tags to be inverted?

img

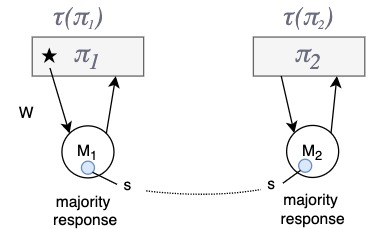
  • \(\tau(\pi_1) \leq \tau(\pi_2)\) therefore \(\pi_1 \leq \pi_2\)
  • \(\exists s \in M_1 \cap M_2\)
  • \(\tau(\pi_2)\) = \(max\{ ts\) from \(M_2\}\)
  • atomicity rule 3: (W) \(\tau(\pi_1) = \tau(\pi_2)\) (R) → we have writer before reader

Multiple writers

The previous is for a single writer case. How to deal with multiple writers in MWMR case? If a writer wakes up it has no knowledge of current state of the system. The writer must learn about the current state.

writer

1
2
3
4
5
6
7
write(v)_i:
  broadcast('R') // pretend to read
  await majority
  choose max tag from acks
  new_tag computation: (maxtag.ts + 1, id)  // id = i
  broadcast('W', new_tag, v)  // to servers
  await majority

server

1
2
3
4
5
6
7
8
upon recv (r):
    send(r_ack, tag, value)

upon_recv(w, tag, val):
  if tag > local_tag then:
    local_tag = tag
    lv = val
  send(w_ack)

If multiple writers operate in the exact same time it is not possible to distinguish writers based on timestamp alone. In this scenario, tag is a pair: \(<ts, id>\) and are compared lexicographically.

Reasoning about behavior: \(s_1, \dots, s_k, a_{k+1}, s_{k+1}\) (similar to induction) → next state maintains properties of the system. → reason about interleavings of the system and consider all possible behaviors. This is in no relation to length of execution; execution may be infinite.

Performance & majorities → Quorums

When waiting for a majority, R/W does a broadcast to \(N\) servers and awaits for majority response. While awaiting the R/W is bombarded with responses and needs to collect \(\frac{N}{2}\) messages which can take a while.

What we actually care about is \(M_1 \cup M_2 \neq \varnothing\).

  • A quorum over set \(S\): any \(Q \subseteq S\)
  • \(\forall Q_i, Q_j: Q_i \cup Q_j \neq \varnothing\)
  • \(|Q_i| = |Q_j|\) and minimal → how small can you get and still maintain a quorum that is equal? \(|Q_i| \geq \sqrt{N} + o(\sqrt{N})\) → but this is hard to construct and not practical

Another strategy:

From a set of servers, form a square. If not possible directly, apply padding. A quorum is a union or row and column = \(R \cup C\).

(the numbers in the grid are servers)

1
2
3
4
5
6
S    ________________________
    |  1  |  2  |  3  |  4  |
Q1: |  5  |  6  |  7  |  8  |
    |  9  | 10  | 11  | 12  |
Q2: | 13  | 14  | 15  | 16  |
     ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾

\(|Q| = \sqrt{N} + \sqrt{N} - 1 = 2 \sqrt{N} - 1\)

  • Wait for response from a \((row, col)\) instead of majority
  • Any quorum intersection response is sufficient

What about failures?

  • in the majority response case, any minority failure model if fine → with quorums much more complicated
  • case about failures: \(f = \sqrt{N}\) can break the system

A bad adversary can kill just the right servers:

1
2
3
4
5
6
S    ________________________
    |  X  |     |     |     |
    |     |  X  |     |     |
    |     |     |  X  |     |
    |     |     |     |  X  |
     ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾     Dead (X _ X).

But as long as a quorum is maintained, the system is fine. This would be OK:

1
2
3
4
5
6
S    ________________________
    |  X  |     |  X  |  X  |
    |     |     |     |     |
    |  X  |     |  X  |  X  |
    |  X  |     |  X  |  X  |
     ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾     NOT Dead (◡ ‿ ◡ ✿)

The motivation for using quorums is not needing to wait for a majority response. Input buffers are a costly resource and quorums help to reduce the need for buffers. Can also design local optimizations for quorums that replay messages to historically responsive quorums.