Skip to content

18. Transition Systems

Mar 15, 2021

Transition systems

Parallel computing: from RAM model → PRAM → async PRAM

Next: distributed computing with message passing and asynchrony:

  • message delays
  • arbitrary local clocks with sequence of execution \(s_0, a_1, s_1, a_2, s_2, a_3,\dots\)
  • execution can be finite or infinite
  • transition is a triplet: \(<s, a, s'>\) (\(s'\) is post-state)
  • on each machine locally:
1
2
3
4
do forever:
  if state in S then:
    s' = a applied to s   // RAM computation
    state = s'

modellings a system this way is called a transition system. Changes to system occur locally, not globally. Actions of the system may be visible or not. For example sending a message is visible to an outside observer, but incrementing a local variable is not.

labelled transition system = actions are labelled and visible from outside

There are two classes of transitions: 1. external = visible from outside to the environment 2. internal = visible only locally, not to any other system component

Components are modeled as a set of transitions.

trace = a projection of execution on external actions

Example of trace

execution: \(S_0\), send, receive, \({i++}\), send...

  • trace: send, receive, send
  • what the world sees and observes about state, and excluding internal actions)

Input/Output Automata (IOA)

  • Introduced in 1989 by Lynch & Tuttle.
  • IOA is a labelled transition system that consists of a signature (actions with types), state, and transitions
  • Initially a mathematical model for distributed systems → later followed by a programming language
  • a transition is modeled in "precondition - effect" form
  • if a state is such that message queue is not empty → take action → change state

Unordered lossless channel

img

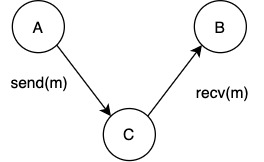
A, B - clients and C - channel

  • the channel provides a service to A, B
  • the channel is unordered and lossless
  • transitions are input/output actions
  • a message interacts between component (A or B) and channel C

signature

  • input: send (\(m\)), \(m \in T\)
  • output: recv(\(m\), \(m \in T\)

state

  • \(M \in\) messages (set), initially \(\varnothing\)

transitions (specified for channel)

  • input \(send(m)\)
    • precondition: true (channel cannot deny service)
    • effect: \(M \leftarrow M \cup {m}\)
  • output \(recv(m)\)
    • precondition: \(m \in M\)
    • effect: \(M \leftarrow M - {m}\)

Notes:

  • if there are multiple components sending specify \(send(m)_{i,j}\)
  • messages are specified in a set → channel is unordered
  • message is removed from set only on delivery → channel is lossless
  • sending increases the set of messages by 1
  • there can be infinitely many transitions

Unordered lossy channel

We can make the previous specification lossy by adding a new transition:

transitions (for channel)

  • input \(send(m) \dots\)
  • output \(recv(m) \dots\)
  • internal \(lose(m)\)
    • precondition: \(m \in M\)
    • effect: \(M \leftarrow M - {m}\)

Note that lose is not visible in the trace; it is internal only and invisible to observer of the system.

Ordered lossy channel

state

  • \(M \in\) messages (queue), initially empty

transitions

  • input \(send(m)\):
    • precondition: true
    • effect: \(M \leftarrow M \circ {m}\) (add to queue)
  • output \(recv(m)\)
    • precondition: \(m = M.first\)
    • effect: \(M \leftarrow M.tail\)
  • internal \(lose(m)\)
    • precondition: \(m = M.first\)
    • effect: \(M \leftarrow M.tail\)

For lossy channel it is sufficient to lose the message some time before delivery (cannot remove message from middle of queue) → lose first messages.

These examples are mathematical definitions of a channel.

Server example

on server - state: \(<lv, lts>\)

1
2
3
4
5
upon recv(w, ts, v):
  if ts > lts:
    lv = v
    lts = ts
    send(w_ack)
  • state: \(<lv, lt, M>\) (where \(M\) is a set of messages)
  • signature:
  • input: \(recv(m)\)
  • output: \(send(m)\)
  • transitions:
  • input \(recv(W, ts, v)\)
    • precondition: true
    • effect: (effect is the code block) 
      1
2
3
      if ts > lts then:
  LV <- v, LT <- TS (*
  M <- M u {send_ack} (**
      *) need to do send_ack but cannot nest actions → add queue to state
      **) then can do send_ack
  • out \(send(m)\)
    • precondition: \(m \in M\)
    • effect: \(M \leftarrow M - {m}\)

To add ability to respond to read messages, specify input \(recv(R,...)\), with precondition and effect. Pattern matching allows distinguishing between reads and writes.

How to model failures on server? Introduce a fail action and send send and receive to check for crash.

  • signature: input fail
  • state: \(<lv, lt, M, crash>\)
  • transitions:
    • input \(fail\):
      • precondition: true
      • effect: crash = true
    • input \(recv(m)\): effect: (add) if !crash && ts > lts then...
    • output \(send(m)\): precondition: (add) \(m \in M\) and not crash

Now we have a server that can fail. Recall safety means nothing bad happens, but since the specification is modeling failures, failures are allowed to happen. IOA models safety not liveness. There is nothing that forces progress. Prove safety, obtain a set of traces then can reason about liveness.