Skip to content

16. Majorities

Mar 8, 2021

Parallel system vs. distributed system:

img

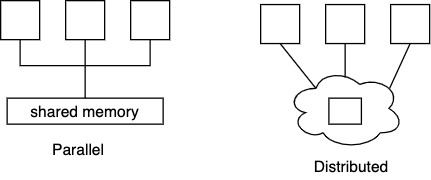
Parallel: memory access operations have no latency (1 cycle) Distributed: no shared memory, uses message passing → memory access latency

Serialization

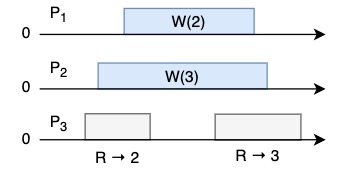
Consider the following read/write flow - what do the reads return?

img

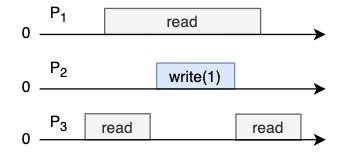
→ depends on what time the serialization points occur

★ = serialization point

img

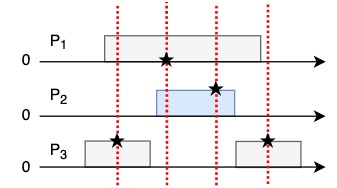
  • \(P_1\) read returns 0
  • \(P_3\) first read returns 0, second read returns 1

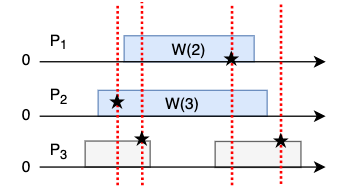
When read is concurrent with write, the read may return 0 or 1, depending on the serialization point Here is an alternative valid serialization where \(P_1\) read will return 1:

img

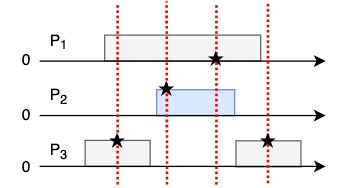
Note that \(P_3\) operations are not concurrent → better return correct values since serialization points are before/after write.

Operation is atomic when it behaves like a sequential execution. If you generalize this to arbitrary object, it is said to be linearizable (by Leslie Lamport). Lineralizability includes atomicity (subset).

Problematic example

Can this be explained as an atomic execution? Where do serializations occur?

img

1
W(3) -> R(3) -> W(2) -> R(2)

img

So far OK.

Add two new read processors, can this still be serialized?

img

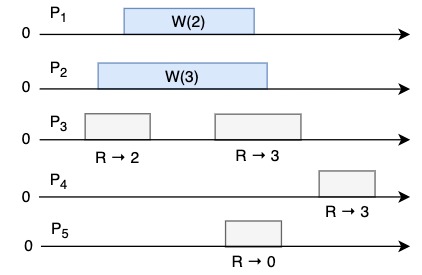
No, because not possible to explain \(P_5\) reading 0 value.

Reader sees the value that was serialized most recently, otherwise it sees the initial value.

Majorities

Given: \(x \in {1...N}\)

1
2
3
4
5
x = 0
PID = 1...N
parbegin
    PID: x++
parend

What is x? Can be anything.

Want a read/write object that is atomic and fault tolerant - obtain atomicity by algorithms and protocols - obtain fault tolerance by redundancy and replication

Consider asynchronous system using message passing. Assume we have \(N=3\) replica servers \(A, B, C\):

img

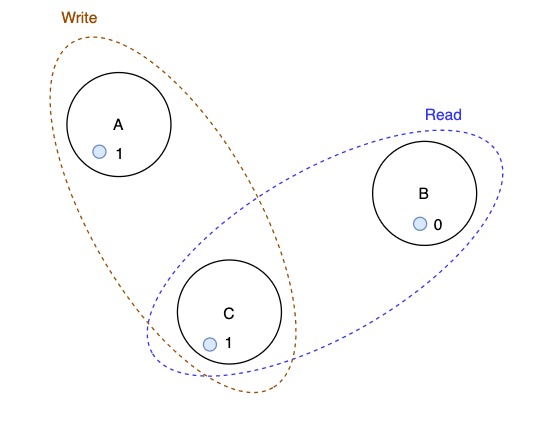
  • Use majorities to determine correct value (atomicity)
    • tolerates minority failures \(f < \frac{N}{2}\) in the system where \(N\) is the number of replica servers
  • write reached majority \(M_1\) notes and will see value 1
  • read will also see majority and will see value 1

No matter which majority is selected: \((A, B)\), \((A, C)\) or \((B, C)\); all include 1.

  • SWMR - single-writer/multi-reader
  • MWMR - multi-writer/multi-reader

img

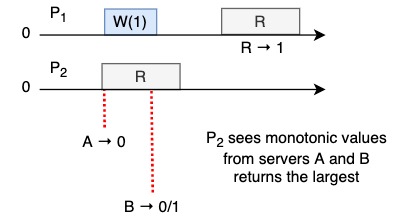
Single writer operation sequence

1
2
3
4
5
<local value, timestamp> = <0, 0>
W: write(v):
    ts += 1
    broadcast('W', v, ts) // to all servers
    await majority responses

Reader operation sequence

1
2
3
4
5
6
7
8
9
C = Ø
broadcast('R') // to all servers
await majority response

upon recv(msg):  // <R, V, T>
  C = {C} union {msg}
  r = msg.v such that msg.ts = max{ msg.ts | msg in C}
  // *) see comment below
  return r

Server operation sequence

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
// awaits messages, has local <lv, ts>

recv(msg):
    if msg.ts > ts && msg.type == 'W':
       lv = msg.v
       ts = mgs.ts
       send(w_ack)  // write acknowledgement
    if msg.type == 'R':
        m.t = ts
        m.v = lv
        send(r_ack, m) // read ack

(* There is an issue with long writes → readers help writer and broadcast the value 1 — "readers must write". We will continue with this algorithm later to see how this works.)