Skip to content

15. Simulation

Mar 3, 2021

Task semantics

Recall PRAM assumes: synchrony, high bandwidth memory, no failures

  • we have looked at how to solve arithmetic, logical, and DO-ALL problems on a PRAM
  • DO-ALL problems are independent, similar and idempotent

Types of task semantics

  • at least once semantics - must perform task at least once
  • exactly once semantics - much harder; if processor completes task but fails immediately after, no other processor should do the task
  • at most once semantics - similar to voting; task will be done \(0...1\) times.

Simulation

Next consider a scenario where task depends on completion of the previous task: "PRAM lifecycle" - each follows RAM instruction set (von Neumann model), PRAM performs following operations:

  • (fetch next instruction)
  • read
  • compute
  • write
  • next (fetch the instruction to perform then do it)

Sample Program

Command Steps
load read, next + 1
store write, next + 1
incr read, compute, write, next + 1
jump set addr to program counter

All processors execute this lifecycle in a synchronous way. Assume 4 processors:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
P: [1]  [2]  [3]  [4]
   ------------------
    F    F    F    F  <-- do all
   ------------------

   ------------------
    R    R    R    R  <-- do all
   ------------------

   ------------------
    C    C    C    C  <-- do all
   ------------------

   ------------------
    W    W    W    W  <-- do all
   ------------------

   ------------------
    J    J    J    J  <-- do all
   ------------------

Each step is a do-all computation. What happens is a processor is asynchronous?

Consider using two generations of memory

img

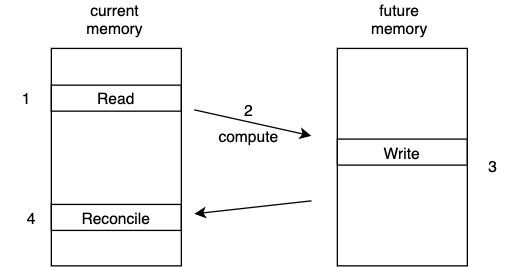
In step 4: reconcile memory by copying any changes to the original (current) memory.

This strategy requires memory allocation 2x the number of possible writes.

(See chapter on simulation for details)

This memory model allows simulating any failure-prone PRAM model.

Analysis

How expensive is 1 step of ideal PRAM?

  • \(N\) = number of virtual processors
  • \(P\) = number of real processors
  • \(Time = 1\)
  • \(Work = N\)

Cost of emulation: need to evoke the do-all problem, there are possibly crashes

  • will not know time, depends on number of crashes
  • \(W = W_{DO-ALL}(N, P) = O(N + P(\frac{\lg^2 N}{\lg \lg N}))\)
  • \(T\) steps: \(W_T = T \cdot W_{DO-ALL}(N, P)\)
  • with asynchronous model with crash and restart: \(W = O(N \cdot P^{0.59})\)

Message Passing Systems

Algorithms in read/write system are simpler than send/receive models. What we want:

  • distributed system: must make it fault tolerant → solve with redundancy
  • shared memory that behaves like local memory: consider the semantics of ER/EW/CR/CW: this is a synchronous PRAM model; even worse in this case since must deal with consistency of memory over time
  • linearizability/atomicity - operations are indivisible; including read/write from the observer perspective

Consider this client-server model:

img

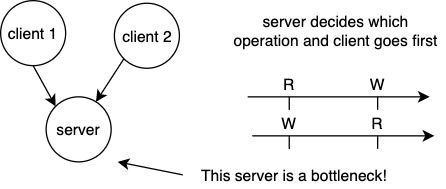
Note if the server fails, then the entire system fails. We can replicate the server which raises another issue: how to propagate values between servers?

Few bad options (not fault tolerant): Read all/write all; read all, write one

Better strategy: use read/write majority

img

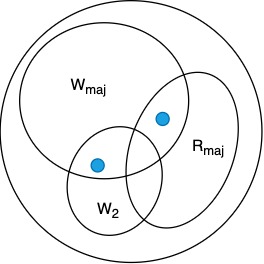
  • if the operations are disjoint in time (read/write operations are not concurrent), there is a mathematical likelihood these match
  • this strategy tolerates minority failures
  • need timestamps to distinguish \(W_1\) from \(W_2\) → pick value based on maximum timestamp