14. Groote Algorithm
Mar 1, 2021
Algorithm X (cont.)
Recall when \(N = P\) algorithm X has work complexity \(W = O(N^{1.59})\). Next consider case where \(P \leq N\).
Subtree strategy
First solve the problem for \(P\) processors, and continue until the subtree is done:
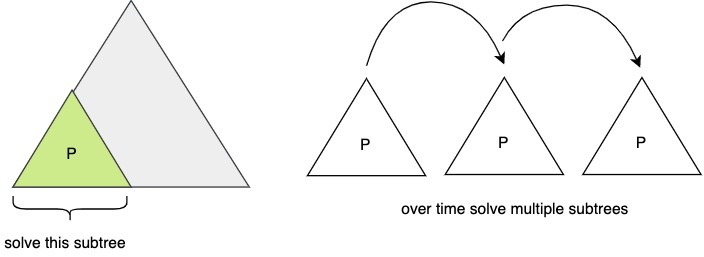
(\(log_{2}3-1 = log_23- log_22 = log_2\frac{3}{2}\))
\(= O(T_1^* \cdot P^{0.59})\). This is polynomial work efficiency.
Polynomial when \(W = O(T_1^* \cdot N^\epsilon)\) where \(0 < \epsilon < 1\). Also remember solutions of interest are between \(N \lg N\) and \(N^2\).
Chunking strategy
Split into 2 subtrees. One will be done first. Then send all processors to the remaining side. (doppelganger effect).
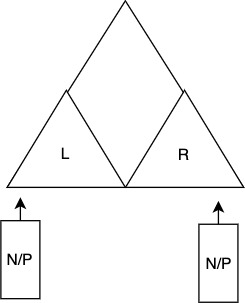
for use soon: \(3^{\log_2P} = P^{\log_23}\)
(some mistake here; should be \(\log_2^{\frac{3}{2}}\) since 0.59)
\(W_{\frac{N}{P},1} = O(\frac{N}{P})\)
Same result, which is better? If there are no failures: - subtree strategy: \(W = P \log P \cdot \frac{N}{P} = N \log P\) - chunking strategy: \(W = \frac{N}{P} \cdot \log P \cdot P = N + P \log P\) (better)
New Notion for Optimality
If work of an algorithm is \(W_{P, N} = (T_1^*) + o(N)\).
\(\lim_{n \to +\infty} \frac{f(N)}{N} \to 0\)
Measure in precise units DO-ALL \(W_{P,N} = N + o(N)\).
Algorithms of this complexity are optimal.
Groote Algorithm
This is a collision based DO-ALL algorithm.
Case: 2 processors
Setup: \(P = 2\), \(N\) tasks to complete
Trivial solution: both processors do all tasks, \(W = 2N = O(T_1^*)\).
Another strategy:
- two processors start from opposite ends of array.
- when finished with task, set bit-array to 1
- check next bit and do work until collision
- if at collision both see 1, the last task is done twice
\(W_{P2} = N + 1\)
Case: 3 processors

Work on 1 half is: \(W_R = \frac{N}{2} + 1\)
After the collision, the middle processor works exclusively in one direction. The end jumps in the middle of the remaining half.
\(W_N = \frac{N}{2} + 1 + W_{left} = \frac{N}{2} + 1 + W_{\frac{N}{2}}\)
Solve this recurrence:
\(= \frac{N}{2} + 1 + ({\frac{N}{4}} + 1 + W_\frac{N}{4})\)
\(= \frac{N}{2} + \frac{N}{4} + 2 + ({\frac{N}{8}} + 1 + W_\frac{N}{8})\)
\(= \sum_1^k \frac{N}{2} + k + W_\frac{N}{2^k}\)
\(= N \cdot \sum_1^\infty \frac{1}{2} + \log_2N + W_1\)
This recurrence is done when \(\frac{N}{2^k} = 1\) or \(k = log_2N\). Work of 1 processor is \(W_1 = O(3)\).
\(= N + log_2N + 3\)
\(= N + o(N)\) ← this is optimal
This strategy works for a few processors, but becomes tedious when number of processors increases.
Case: \(P = 2^k\) processors
| k | P | W |
|---|---|---|
| 1 | 1 | \(W= N +1\) |
| 2 | 4 | \(W = N^2 + \sqrt{N} + 1\) |
| 3 | 8 | \(W = (M + 1)3\) |
| d | \(2^d\) | \(W_d = (M + 1)^d\) |
Example k=2: 4 processors
Divide processors into 2 groups. There are \(M \times M = N\) tasks.
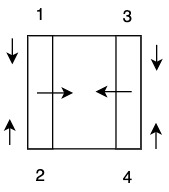
Processors work vertically on each slice. Ultimately a collision occurs.
\(W_{pair} = W_p = M+1\) - for doing 1 vertical chunk
\(W_{total} = W_{col} \cdot (M+1) = (M + 1)(M + 1) = M^2 + 2M + 1\)
\(= N + 2 \cdot \sqrt{N} + 1 = N + o(N)\) ← optimal
Example k=3: 8 processors
Divide processors into groups of two and work on a cube from both directions
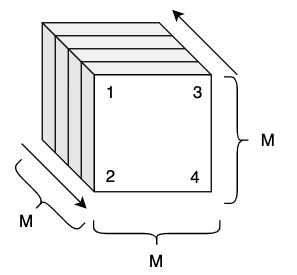
\(M^3 = N\) and \(N^{1/3} = M\)
\(W_{slice} = (M+1) = N + 2 \cdot \sqrt{N} + 1 = (M+1)^2\)
\(W_{total} = (M+1)^2 (M+1) = M^3 + 3M^2 + 3M + 1\)
\(= N + 3N^\frac{2}{3} + 3N^\frac{1}{3} + 1\)
\(= N + o(N)\)
Example k=4: 16 processors
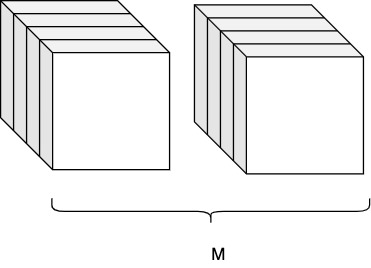
\(N = M^4\) and \(N^\frac{1}{4} = M\)
\(W = W_{P8} \cdot (M+1) = (M + 1)^4\)
\(= N + 4N^\frac{3}{4} + 6N^\frac{2}{4} + 4N^\frac{1}{4} + 1\)
\(= N + o(N)\)
Notice: each time we increase \(k\) the coefficients increase. The result is a sum that does not converge.
In the general case \(k = d\): \(P = 2^d\) \(N = M^d\) and \(W_d = (M+1)^d\)
Example k = d
\(d =\) dimensions, \(P = 2^d\) and \(N = M^d\), \(d = \log_{2}P\)
\(W_d = (M + 1)^d = (M + 1)^{\log P} = \frac{N}{N} (M+1)^{\log P}\)
\(= N \cdot M^{\frac{1}{d}} \cdot (M+1)^{\log_2P}\)
\(= N \cdot (\frac{M + 1}{M})^{\log_2P}\)
\(= N \cdot P^{\log2(\frac{M + 1}{M})}\)
If \(M = 1\) then \(N=1\) and \(1 \cdot P^{\log_2\frac{2}{1}} = P\).
If \(M \to \infty\) then \(W \to N\).
If \(M = 2\) then \(W_d = N + P^{\log_2\frac{3}{2}}\) ← polynomially efficient