Skip to content

12. Optimized W

Feb 22, 2021

Algorithm W: Block Step (cont.)

Recall block step:

1
2
3
4
5
while progress tree root != N do:
    1. enumerate
    2. load balance
    3. do task at leaf
    4. estimate progress

img

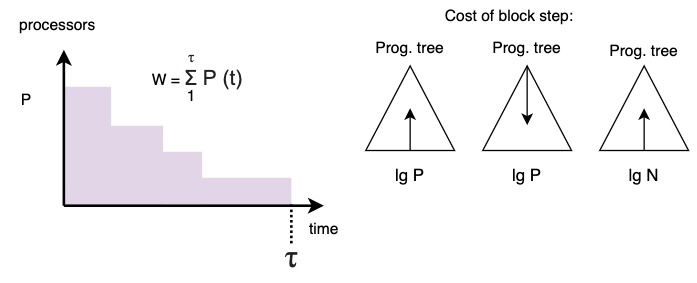
\(W = 1 \cdot \sum P (T)\)

Cost of block = \(\Theta(\lg N + \lg P)\)

\(\sum P(t) = B_1 + B_{2a} + B_{2b}\), where for \(B_1\), \(u_j \leq P_j\).


\(B_{2a} = U_j < P_j\) and \(U_{j+1} \leq \frac{U_j}{\lg N/\lg \lg N}\). - This can happen at most \(k = O(\frac{\lg N}{\lg \lg N})\) → \(O(P \frac{\lg N}{\lg \lg N})\) times.


\(B_{2b} = U_j < P_j\) and \(U_{j+1} > \frac{U_j}{\lg N/\lg \lg N}\) (massive failures). - This can happen at most \(O(P \frac{\lg N}{\lg \lg N})\) times.


Per task / number of tasks:

\[ U_j - U_{j+1} \leq U_j - \frac{U_j}{\lg N / \lg lg N} = U_j (1 - \frac{1}{\lg N / \lg \lg N}) \]

Work in iteration: (*) from here

\[ \frac{P_j}{U_j}(U_j - U_{j+1}) \leq \frac{P_j}{\cancel{U_j}} \cdot (\cancel{U_j})(1 - \frac{1}{\lg N / \lg \lg N}) \]

Crashes:

\[ U_{j+1} \cdot \frac{P_j}{U_j} > \frac{\cancel{U_j}}{\lg N / \lg \lg N} \cdot \frac{P_j}{\cancel{U_j}} \\ = \frac{P_j}{\lg N / \lg \lg N} \]

Sum of crashes \(j < P\):

\[ = \frac{P_1}{\lg N / \lg \lg N} + \frac{P_2}{\lg N / \lg \lg N} + \dots \]
\[ = \frac{P}{\lg N / \lg \lg N} + \frac{P}{(\lg N / \lg \lg N)^2} + \dots = \sum_1 \frac{1}{x^i} \]

Solve for \(k\)

\[ \frac{P}{(\lg N / \lg \lg N)^k} = 1 \]
\[ P = (\lg N / \lg \lg N)^k \\ lg P = k \Theta(\lg \lg N) \]
\[ k = \Theta(\frac{\lg P}{\lg \lg N}) \]

Solve cost of case \(B_{2B}\) (*) use here

\[ B_{2b} = \sum_{j}^{k} \cdot P_j(1 - \frac{1}{\lg N/\lg \lg N}) \leq P \sum_{j}^{k}(1 - \frac{1}{\lg N/\lg \lg N}) \]
\[ = P(\frac{\lg N}{\lg \lg N})(1 - \frac{1}{\lg N/\lg \lg N}) \]
\[ = O(P(\frac{\lg N}{\lg \lg N})) \]

Total cost of cases:

\[ B = B_{1} + B_{2a} + B_{2b} = O(N + P \frac{\lg N}{\lg \lg N} + P \frac{\lg N}{\lg \lg N}) \]

\(P \leq N\), Cost of blocks: \(\Theta(\lg N + \lg P) = \Theta(\lg N)\).

Work is \(W = Cost_{BC} \times\) num_blocks

\[ = O(N \cdot \lg N + P(\frac{\lg^2N}{\lg \lg N}) + P(\frac{\lg^2N}{\lg \lg N}) \]
\[ = O(N \cdot \lg N + P(\frac{\lg^2N}{\lg \lg N})) \]

→ the dominant term is \(P(\frac{\lg^2N}{\lg \lg N})\) and \(T_1^* = \Theta(N)\); this is not optimal, but it is polylog efficient.

Cost of block step:

\[ Cost_{BS} = \Theta(\lg P + \lg N + 1 + \lg N) = \Theta(\lg N) \]

Optimized Algorithm W

If there was an oracle:

\[ W_{oracle} = O(N + P \frac{lg N}{\lg \lg N}) = O(N \frac{lg N}{\lg \lg N}) \]

Lower bound:

\[ LB_{DOALL} = \Omega(N \frac{lg N}{\lg \lg N}) \]

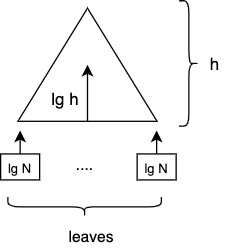
Now modify step 3: do work → instead of 1 task, do \(lg N\) tasks:

\(Cost_{BS} = \Theta(\lg P + \lg N + \lg N + \lg N)\)

img

\(P \leq N\). For which P is this optimal? Substitute \(P = \frac{N}{\lg N}\):

\(W = O(N \lg N + P (\frac{\lg^2N}{\lg \lg N})))\) then \(W = O(N \lg N)\).

\(H = \frac{N}{\lg N}\),   \(B_H = O(H + P\frac{\lg H}{\lg \lg H})\)

\(Cost_{BS} = \Theta(\lg P + \lg H + \lg N + \lg H) = \Theta(\lg N)\)

Needed when estimating work:

\(lg H= \lg N \cdot \lg \lg N = \Theta(\lg N)\)

\(\lg \lg H = \Theta(\lg lg N)\)

Work:

\(Work = B_H \cdot C_{BS} = O(H \lg N + P\frac{\lg H \lg N}{\lg \lg H}) = O(N + P \frac{\lg^2N}{\lg \lg N})\)

Optimal when \(P \leq \frac{N}{\frac{\lg^2 N}{\lg \lg N}}\)

Source routing

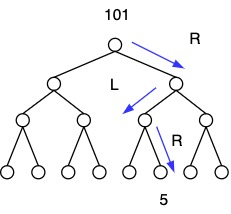
If you have PID = 5, how to find leaf?

Convert it to binary, \(5 = 101\) then use the binary to navigate from root to leaf:

1 - Go right

0 - Go left

1 - Go right

101 = RLR. This only works for 0-based indices.

img