11. Crashes

Feb 17, 2021

Working with Crashes in PRAM

Processor enumeration: use an enumeration tree (e-tree), then run prefix sum on the processors. Enumeration produces and overestimate if processors crash.

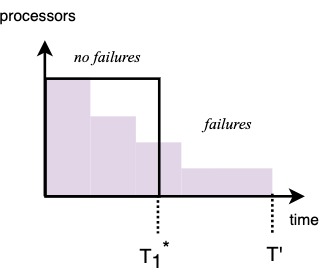
When no failures occur: time: \(\Theta(\lg P)\), work: \(\Theta(P \lg P)\)
With failures: same time, less work gets done. Over time, work increases.

Work is optimal when \(\sum PT = P \cdot T_P = O(T_1^*)\).

Progress estimation: do bottom-up sum. If all tasks are not done, enumerate the processors that are left and load balance → compact processors into a more compact range. To load balance, go top to down along the same tree.

Time \(T_P = \lg N\), and work \(W = P \lg P\).

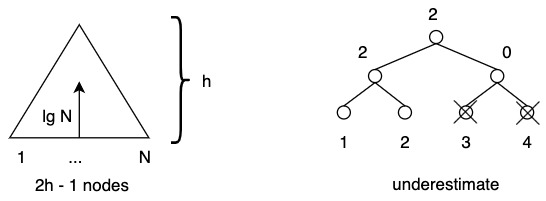
Progress estimate bottom-up sum is an underestimate when processors fail during summation: fewer tasks appear done than actual.

Algorithm W: Block step analysis

Tasks: \(\text{task}[1...N]\), \(N = P\)

for pid = 1...N pardo
    do_task[PID]
    estimate progress
    while progress tree root != N do:
        1. enumerate
        2. load balance
        3. do task at leaf
        4. estimate progress
parend

steps 1.-2. represent the "oracle"
In load balancing step look for leaf with value 0, then do that task
steps 1.-4. combined are called block step

What is the cost of a block step?

\[ T = Step_1 + Step_2 + Step_3 + Step_4 \\ = \Theta(\lg P) + \Theta(\lg N) + 1 + \Theta(\lg N) \\ = \Theta(\lg P + \lg N) \]

Allocating work is negligible if the task is large.

How many block steps do we need? If the number block steps is known, we can compute \(B_{N,P} = BS \times \Theta(\lg P + \lg N)\) and be done.

Handout pg. 147, lemma 10.23: The number of block steps of algorithm W using \(P\) processors on input size \(N\) and using a progress tree with \(N\) leaves, is

\[ B_{N,P} \leq N + \frac{P \lg N}{\lg\lg N} \]

for \(P \leq N\).

Notation	Iteration \(j\)	End of Iteration \(j\)
Iteration	\(j\)	\(j + 1\)
Overestimate of active processors	\(P_j\)	\(P_{j+1}\)
Remaining unvisited leaves	\(U_j\)	\(U_{j + 1}\)

From Lemma 10.20: \(P_j \geq P_{j+1}\) (crash failures)
From Lemma 10.22: \(U_j > U_{j+1}\) (at least 1 task left)
Final iteration of algorithm: \(\tau\)
number of unvisited elements: \(U_\tau > 0\)
After iteration \(\tau\), number of unvisited elements: \(U_{\tau+1} = 0\)

Investigate 3 cases

Case 1: fewer processors than tasks

\(P_j < U_j\) - there are fewer processors than unfinished tasks.

Each leaf will be assigned no more than 1 processor.

Number of block steps will be no more than:

\[ B_{Case1} \leq \sum_{j = 1}^{\tau} (U_j - U_{j+1}) = U_1 - U_{\tau+1} = N - 0 = N \]

Case 2a: lots of progress, few failures

\(P_j \geq U_j\) - there are at least as many processors as tasks

\(\displaystyle U_{j+1} < \frac{U_j}{\log N/\log\log N}\)

Can occur no more than \(O(\log N/\log \log N)\) times, because \(U_{j+1} < U_j = N\).

No more than \(P\) processors complete such block steps, therefore total number of block steps is no more than:

\[ B_{Case2a} = O(P \frac{\log N}{\log \log N}) \]

Case 2b: many failures and slow progress

\(P_j \geq U_j\) - there are at least as many processors as tasks

\(\displaystyle U_{j+1} \geq \frac{U_j}{\log N/\log\log N}\)

By Lemma 10.21, number of assigned processors is no less than \(\lfloor{\frac{P_j}{U_j}}\rfloor\) and no more than \(\lceil{\frac{P_j}{U_j}}\rceil\).

Number of failed processors is at least:

\[ U_{j+1} \lfloor{\frac{P_j}{U_j}}\rfloor \geq \frac{U_j}{\log N/\log \log N} \cdot \frac{P_j}{2U_j} \geq \frac{P_j}{2 \log N / \log \log N} \]

and at most \(\tau\) times.

Number of processors completing step \(j\) is at most/no more than:

\[ P_j(1 - \frac{1}{2(\log n/\log\log N)}) \]

In general, for \(P\) initial processors, number of processors completing \(l^{th}\) occurrence of case 2b is no more than:

\[ P(1 - \frac{1}{2(\log n/\log\log N)})^l \]

The number of block steps in case 2b is bounded by:

\[ B_{Case2b} \leq \sum^{\tau}_{l = 1} P(1- \frac{1}{2(\log N/\log\log N)})^l \\ \leq P \cdot \sum^{\infty}_{l = 1} (1- \frac{1}{2(\log N/\log\log N)})^l \]

\[ = P\frac{1}{1 - (1- \frac{1}{2(\log n/\log\log N)}}) \]

\[ = P \cdot 2(\frac{\log N}{\log \log N}) \]

\[ = O(P (\frac{\log N}{\log \log N})) \]

Total block steps

Total number of all block steps for all cases is

\[ B_{N, P} = B_{Case1} + B_{Case2a} + B_{Case2b} = O(N + P \frac{\log N}{\log \log N}) \]