Skip to content

10. Redundancy

Feb 15, 2021

Redundancy

  • we can achieve fault tolerance through redundancy
  • redundancy conflicts with efficiency
  • There are two types of redundancies
    1. space redundancy, e.g. spare tire
    2. time redundancy e.g. dual rail ethernet, parity memory
  • Other examples of redundancy
    • retransmission of network messages (time)
    • redundant arrays of independent disks (RAID)
    • N-version programming: develop multiple versions of the same program to solve the same problem and choose majority result → tolerates minority failures

Consider a decentralized system of \(N\) processors: - 1 processors fails, - now \(N-1\) functional processors - more failures may occur but \(< N\) - we have graceful degradation of service

Assume at least 1 processor survives (\(P-1\))

img

Example: Network Supercomputing

  • SETI@home project: looking for extra terrestial life
  • System with master-worker architecture:
    • master distributes work
    • workers send back processed results

img

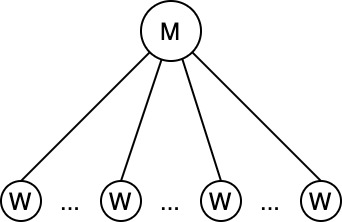
  • Several points of failure:
    • master is a central point of failure
    • workers may be malicious or faulty → master spends ~70% of its time validating processed results
  • Redundancy in this system:
    • time: master spends time to check same answers repeatedly
    • space master sending same task to multiple workers (because they may fail or be malicious)
  • This is a DO-ALL problem: there are N tasks and P processors - recall:
    1. tasks must be similar (same chunk size)
    2. tasks must be independent
    3. tasks must be idempotent

DO-ONE Problem

  • We have \(N=1\), \(P > 1\) and \(failures \leq P-1\) (at least 1 processor remains)
  • Task: write X := 1 to shared memory

One strategy:

  • keep a task queue \(TASK[1...N]\), and
  • keep a done queue \(DONE[1...N]\)
  • then: if not done task[i] then do task [i]

On a CRCW PRAM

1
2
3
x = 0
for PID 1...P pardo:
    DO TASK(1) // x := 1
  • \(T_P = 1\) task
  • \(W = P \cdot T_P = \Theta(P)\)
  • \(T_1^* = O(1)\)

On a CREW PRAM

  • Attempt to write X:=1 to shared memory P times will generate ~ \(P-1\) runtime errors
  • On CREW PRAM must use both space and time redundancy
1
2
3
4
5
x = 0
for PID 1...P pardo:
    for i = i...P:
        if pid == i:
           then x:= 1
  • \(T_P = \Theta(P)\)
  • \(W = P \cdot T_P = \Theta(P^2)\)

These are not good values for time and work → CREW/CRCW are not good models for studying fault tolerance

CRCW Matrix Maximum

Goal: Compute array/matrix max in \(O(1)\) time

Basic approach: - compute max of \(X[1...N]\) - make a binary tree and initialize leaves to values of \(X\) - iterate over tree height: - if left child >= right child, store left child value at parent - if right child > left child, store right child value at parent - Time: \(T_P = \lg N\) - Work: \(W_P = \Theta(N \lg N)\) - note: this is similar to a real-life elimination tournament

Next: all play all tournament

img

  • Number of comparisons is \(N^2\)
  • Two games between each → matrix is not symmetric \(X_{ij} \neq X_{ji}\)
  • Assign processor to each slot: \(T_P = 1 = \Theta(1)\)
1
2
3
4
5
for PID = 1...P pardo
    if x[i] > x[j] then
        R[i] = 1
    else
        R[i] = 0

Steps 1. Do round robin on (as above) - \(\Theta(1)\) 2. Do logical AND on the matrix rows - \(\Theta(1)\) 3. Determine result:

1
2
3
4
5
for PID = 1...P pardo
    if row[i]_AND == 1 then
        max = x[i]
    else
        noop;

If there exists a chance of multiple maximum values use lexicographical pair <X[i], i> instead of simple index.

Number of processors: \(P=N^2\) and \(N = \sqrt{P}\)

Bounds
\(T_1^*(N) = \Theta(N)\) Uniprocessor
\(T_P = \Theta(1)\) Parallel time
\(S = \frac{T_1^{*}(N)}{T_P} = \frac{\Theta(N)}{\Theta(1)} = \Theta(N) = \Theta(\sqrt{P})\) Speedup
\(W_P = P \cdot T_P = N^2 \cdot \Theta(1) = N^2\) Work

Note - Speedup: \(\Theta(\sqrt{P}) \neq \Theta(P)\) → not linear! - Work: \(W_P \gg T_1^*(N)\)

Progress Trees

img

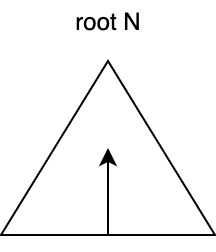
  • Given \(N = P\)
  • iterate bottom to top
  • general idea:
    1. at PID: do task[PID]
    2. progress estimate

While root of progress tree is \(\neq N\): 1. enumerate processors 2. load balance using progress tree 3. do the task at leaf 4. compute progress estimate

...more on this later.