Algorithm Groote

for asynchronous systems
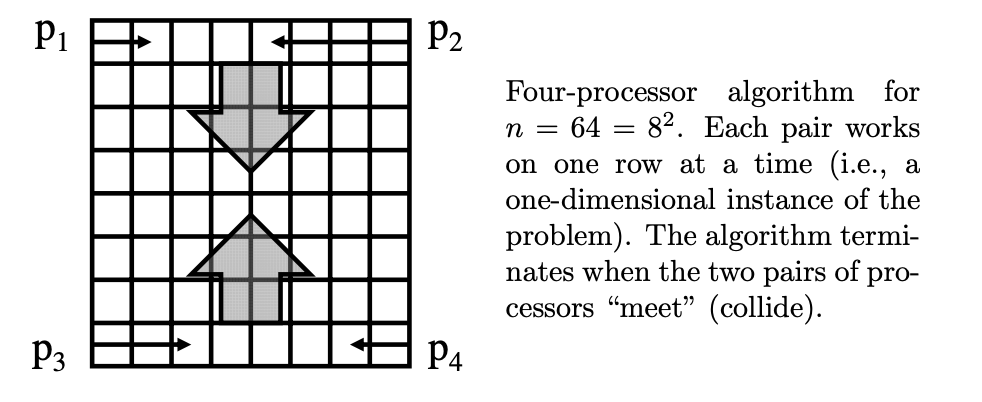
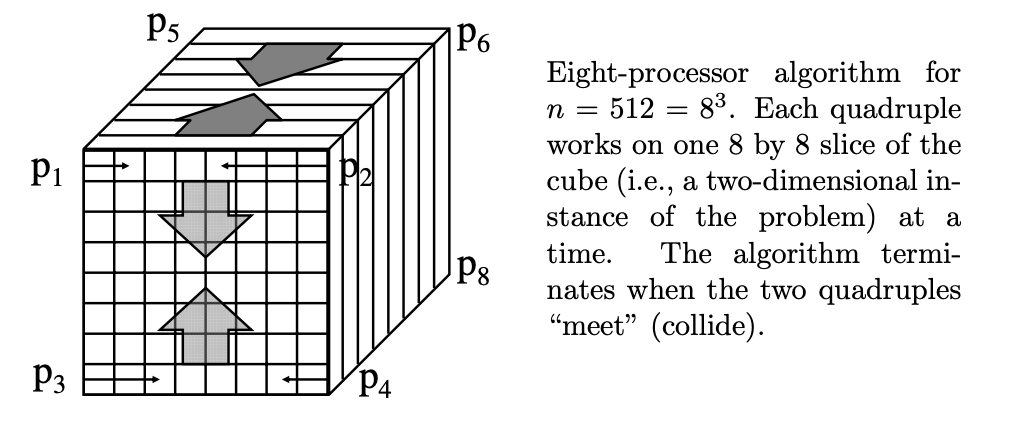
solves DO-ALL with $n = m^{k}$ tasks and $P = 2^{k}$ processors ( $P \leq N$ ) for some parameter $m$ and constant $k > 0$
Processors complete tasks sequentially until detecting a collision
Each processor stops when it inspects a task that has already been performed by the other processor
$C_{2}$ = cost of work performed by two processors → at most $n + 1$ when $m = 2$
in the general case: processors work in opposing groups, on $k - 1$ dimensional slices, on a $k$ size cube

m=4

m=8

(no pseudocode available)

Complexity

Analysis
Work, $P \geq N$	$O (N P^{c})$ where $0 < c = \log (\frac{m + 1}{m}) < 1$
Duplicated work	$C_{P} = (m + 1)^{k}$
Cost of checking task completion	$R = O (N \log P)$